Parametrische versus nichtparametrische Tests
In der induktiven Statistik wird grundsätzlich unterstellt, dass die beobachteten Daten Realisationen von Zufallsvariablen sind.
Parametrische Verfahren
In der parametrischen Statistik wird darüber hinaus unterstellt, dass die Zufallsvariablen selbst aus einer bestimmten Wahrscheinlichkeitsverteilung stammen, diese aber nicht zu 100% bekannt ist. Konkret wird angenommen, dass die "Familie" der Wahrscheinlichkeitsverteilung bekannt ist. Unbekannt sind zunächst also nur die Parameter, die die Verteilungsfunktion exakt bestimmen.
So kann bspw. angenommen werden, dass die Daten aus einer normalverteilten Grundgesamtheit stammen und damit grundsätzlich folgende Formel für die Grundgesamtheit gilt:
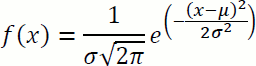
Das "Problem" dabei ist, dass die genaue Verteilung erst durch die beiden Parameter µ (Erwartungswert) und σ (Streuung) bzw. σ2 (Varianz) festgelegt wird, und die Verteilung je nachdem, welche Werte diese Parameter annehmen, höchst unterschiedlich aussieht.
Die nächsten Beispiele sollen dies veranschaulichen.
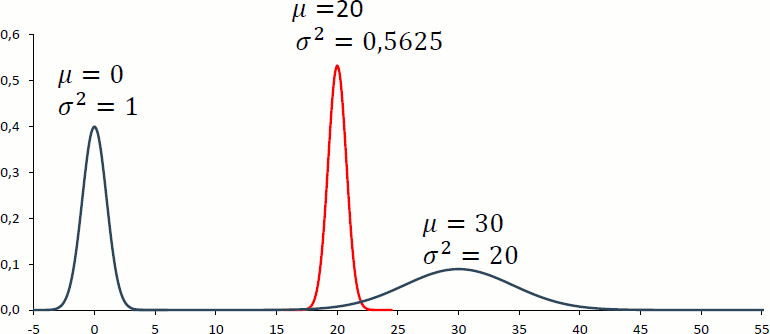
Die Kenntnis über Form (und Lage) der Wahrscheinlichkeitsfunktion ist aber deshalb von Bedeutung, weil nur so die Frage beantwortet werden kann, wie hoch die Wahrscheinlichkeit ist bspw. einen Wert von 30 (oder kleiner) zu beobachten. Gelten die Parameterwerte der Verteilung ganz rechts, so beträgt diese Wahrscheinlichkeit exakt 50%. Gelten die anderen Parameterwerte, dann ist die Wahrscheinlichkeit praktisch 0%.
Daher müssen in der parametrischen Statistik die Werte für µ und σ2 aus vorliegenden Daten geschätzt werden, weil nur so Wahrscheinlichkeitsaussagen möglich sind.
Nichtparametrische Verfahren
In der nichtparametrischen Statistik wird keine Verteilungs"familie" unterstellt, weshalb auch keine Parameter geschätzt werden müssen. Daher werden diese Verfahren verteilungsfrei bzw. eben nichtparametrisch genannt. Aber auch bei nichtparametrischen Tests müssen bestimmte Annahmen erfüllt sein.
Im Vergleich zu parametrischen Verfahren sind nichtparametrische Verfahren damit "voraussetzungsfreier", aber nicht voraussetzungsfrei.