Kovarianz
Zusammenhangsmaße sind - wie der Name schon sagt - Maße, mit deren Hilfe der Zusammenhang zwischen Merkmalen beschrieben werden kann. In der Praxis häufig anzutreffen sind:
- Kovarianz
- Korrelation (nach Pearson oder Spearman)
Was die Idee hinter der Kovarianz ist und wie sie den Zusammenhang zwischen zwei metrisch skalierten Merkmalen "findet", soll ein Beispiel zeigen. Die konkreten Daten zum Nachrechnen sind der Tabelle zu entnehmen.
| # | Merkmal A | Merkmal B |
|---|---|---|
| 1 | 1 | 0,8 |
| 2 | 2 | 1,6 |
| 3 | 2,5 | 2 |
| 4 | 2,6 | 2,08 |
| 5 | 2,7 | 2,24 |
Vorab soll ein Streudiagramm (engl. Scatter plot) einen ersten visuellen Eindruck vom Zusammenhang vermitteln. Wie wir sofort erkennen können, ist dieser ziemlich klar.
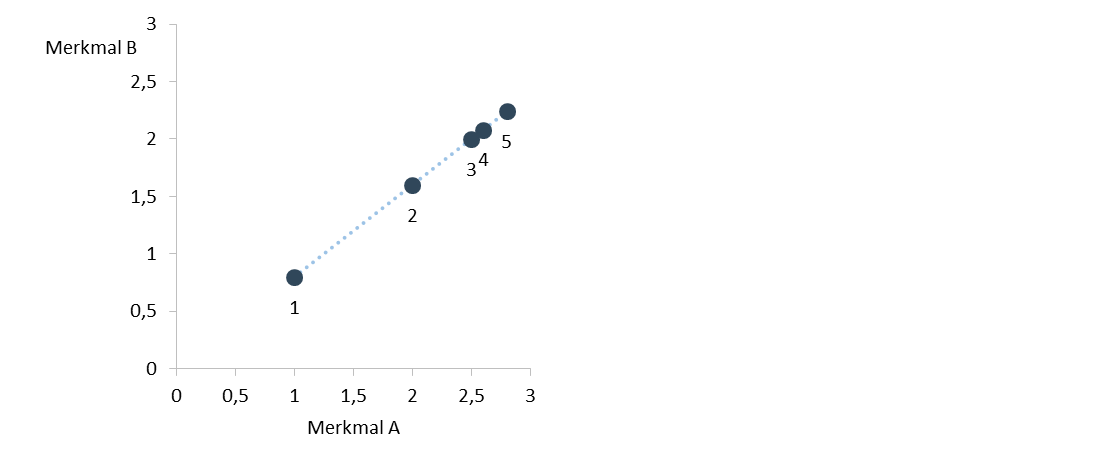
Der Zusammenhang zwischen den beiden Merkmalen A und B ist perfekt. Perfekt in dem Sinne, als dass alle Punkte auf einer gedachten Geraden liegen. Diese Linie wiederum kann so interpretiert werden, dass (egal von welchem Niveau Sie ausgehen) ein Anstieg von A um 1 Einheit zu einem Anstieg von B um 0,8 Einheiten führt. Die Steigung der Geraden beträgt also 0,8. Und gleich vorweg: Die Kovarianz beträgt +0,334
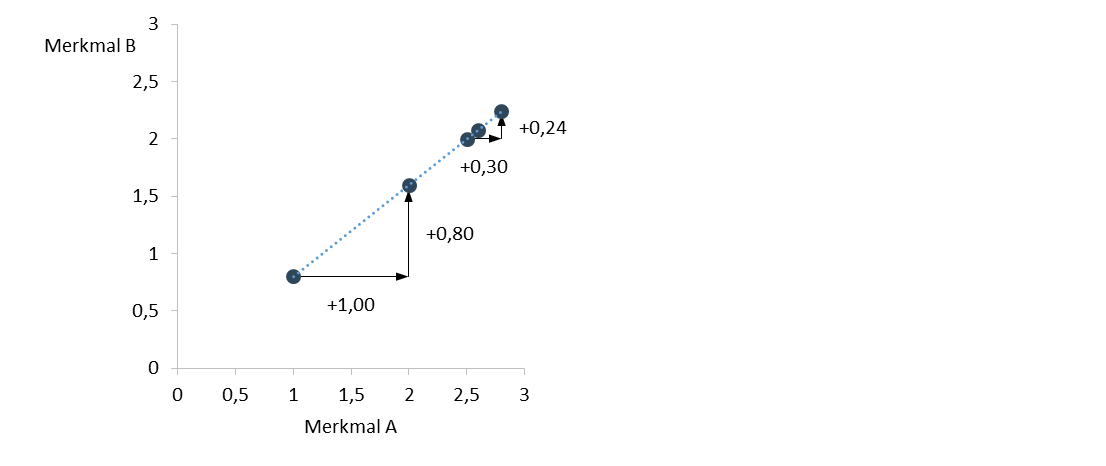
Die Formel zur Berechnung der Kovarianz lautet:
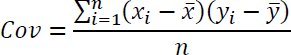
In Worten besagt sie:
- Berechne für jede Beobachtung den horizontalen Abstand der Beobachtung zum Mittelwert der Variable auf der x-Achse.
- Berechne für jede Beobachtung den vertikalen Abstand der Beobachtung zum Mittelwert der Variable auf der y-Achse.
- Multipliziere für jede Beobachtung den horizontalen mit dem vertikalen Abstand.
- Berechne die Summe aus den unter Schritt 3 berechneten Produkten.
- Dividiere diese Summe durch die Anzahl an Beobachtungen.
Wieso diese Formel in der Lage ist lineare Zusammenhänge zu finden, veranschaulicht die nächste Abbildung anhand der 1. und der 5. Beobachtung.
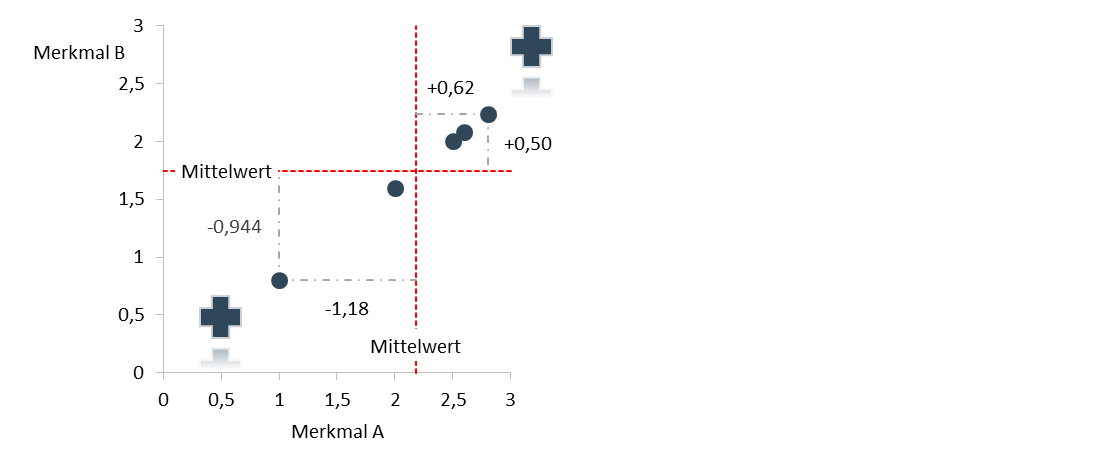
Für beide Beobachtungen gilt, dass das Produkt aus horizontaler mal vertikaler Abweichung positiv ist. Dasselbe gilt für die Beobachtungen 2, 3 und 4.
Weil abschließend noch die Summe gebildet wird und durch die Anzahl an Beobachtungen dividiert wird, ist die Kovarianz letztlich nichts anderes als das mittlere Produkt von Abständen zum jeweiligen Mittelwert.
Im Beispiel beträgt die Kovarianz +0,334 und besagt, dass der Zusammenhang positiv ist. D.h., sie sagt ausschließlich etwas über die Richtung des Zusammenhangs, aber niemals etwas über die Stärke des Zusammenhangs aus.
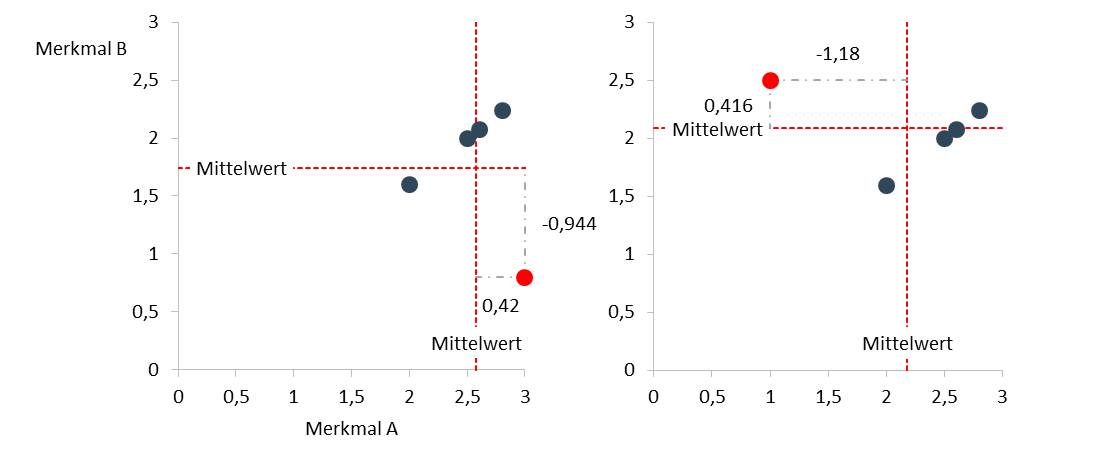
Die nächsten zwei Abbildungen sollen veranschaulichen, wie sich mit dem visuellen Eindruck auch das Vorzeichen der Kovarianz verändert. Im linken Beispiel beträgt die Kovarinaz -0,044 und im rechten -0,067. [1]
Warum wir das Wort linear hervorgehoben haben, soll das nächste Beispiel zeigen.
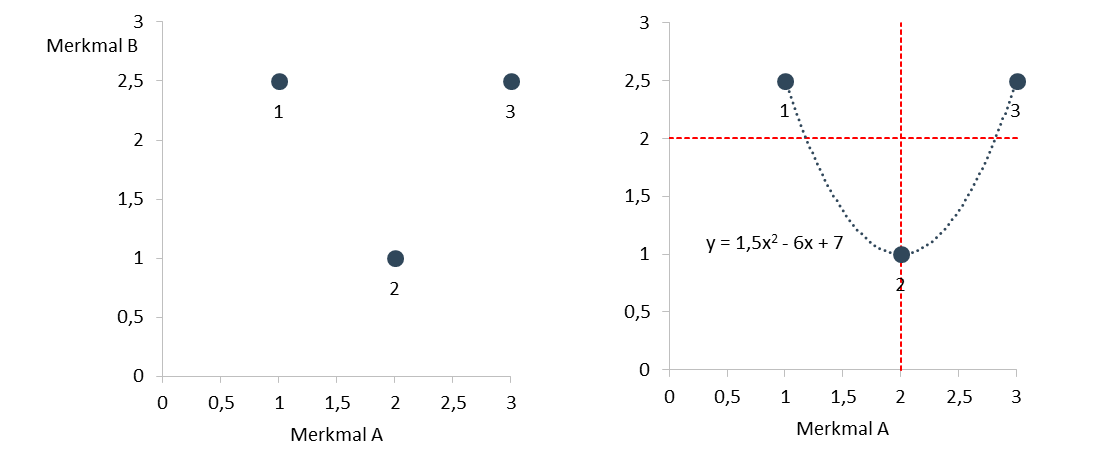
Wie die Abbildung links zeigt, haben wir in diesem Beispiel drei Beobachtungen. Diese drei Beobachtungen können mit einer Linie verbunden werden, und zwar mit einer Linie, die genau durch die in der Abbildung (rechts) angeführte Funktion beschrieben wird. Damit besteht ein perfekter Zusammenhang zwischen Merkmal A und Merkmal B, aber eben kein perfekt linearer Zusammenhang. Die Kovarianz kann diesen Zusammenhang daher auch nicht finden und beträgt Null.
Die zwei Schwachpunkte der Kovarianz veranschaulichen die nächsten beiden Beispiele.
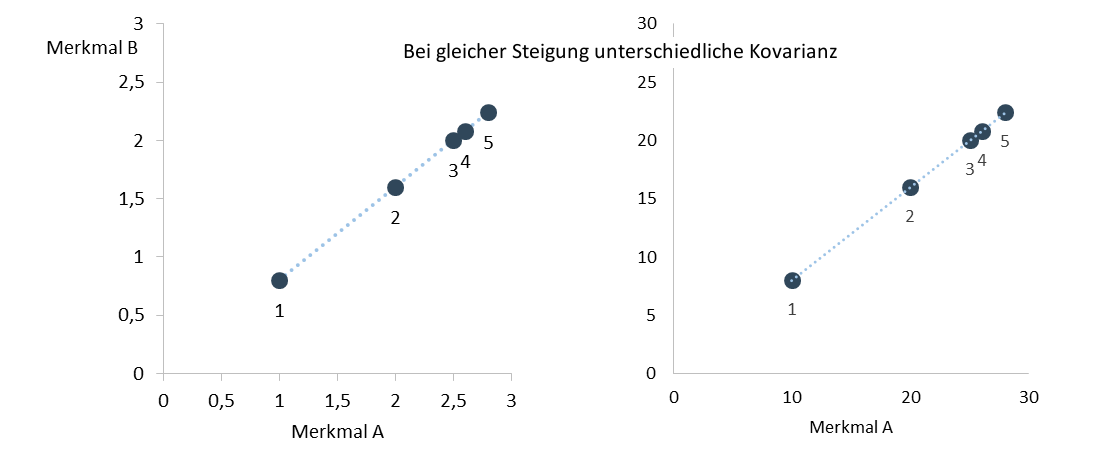
Der erste Nachteil der Kovarianz ist, dass ihr Wert von der Einheit abhängt, in der die Variablen gemessen werden. D.h., es macht einen Unterschied, ob bspw. die Einkommen und Ausgaben von Personen in Euro oder in Eurocent gemessen werden, oder die Körpergröße in Meter oder Zentimeter. Im Beispiel links beträgt die Kovarianz 0,33408 und im Beispiel rechts 33,408 [2].
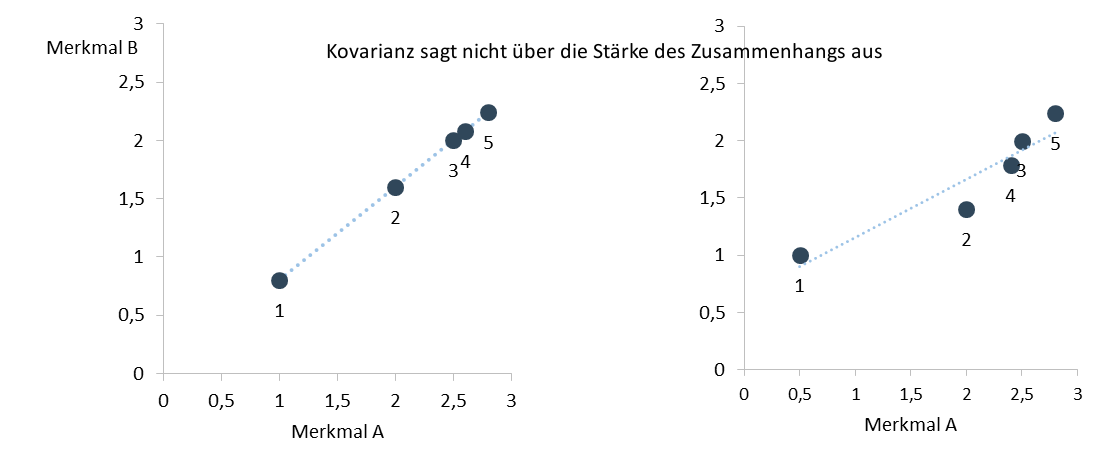
Der zweite Nachteil der Kovarianz ist, dass ihr Wert auch bei unterschiedlich starken Zusammenhängen gleich sein kann, die Kovarianz also nichts über die stärke des Zusammenhangs aussagt. Im Beispiel links und im Beispiel rechts beträgt die Kovarianz jeweils 0,33409.
Fassen wir die Diskussion zusammen.
- Die Kovarianz ist ein Maß für den linearen Zusammenhang.
- Die Kovarianz ist nicht dimensionslos.
- Die Kovarianz sagt etwas über die Richtung des Zusammenhangs aus.
- Die Kovarianz sagt nichts über die Stärke des Zusammenhangs aus.
- Die Kovarianz kann nur berechnet werden, wenn beide Merkmale metrisch skaliert sind.
Umsetzung in SPSS
- Wählen Sie Analysieren ⟶ Korrelation ⟶ Bivariat...
- Unter Optionen... finden Sie die Kovarianz.
[1] Beobachtung 1 wurde dazu horizontal auf 3 bzw. vertikal auf 2,5 verschoben.
[2] Für die rechte Abbildung wurden die Ausprägungen der Merkmale A und B einfach mit 10 multipliziert. Dies hat keinen Einfluss auf die Steigung und den eigentlichen Zusmammenhang. Die Kovarianz verhunderfacht sich dadurch jedoch.