Weiteres Beispiel zur Berechnung der β-Fehler-Wahrscheinlichkeit
Unverbundene Stichproben
Stellen Sie sich alternativ vor, dass die wahre durchschnittliche Karenzdauer bei 17 Monaten liegt und damit die untere Verteilung die richtige ist.
Da Sie weiterhin annehmen, dass die obere Verteilung mit einer durchschnittlichen Karenzdauer von 15 Monaten die richtige ist, würden Sie immer dann, wenn Sie eine Stichprobe ziehen, deren Mittelwert zwischen 7,2 und 22,8 Monaten liegt, die (falsche) Nullhypothese nicht verwerfen.
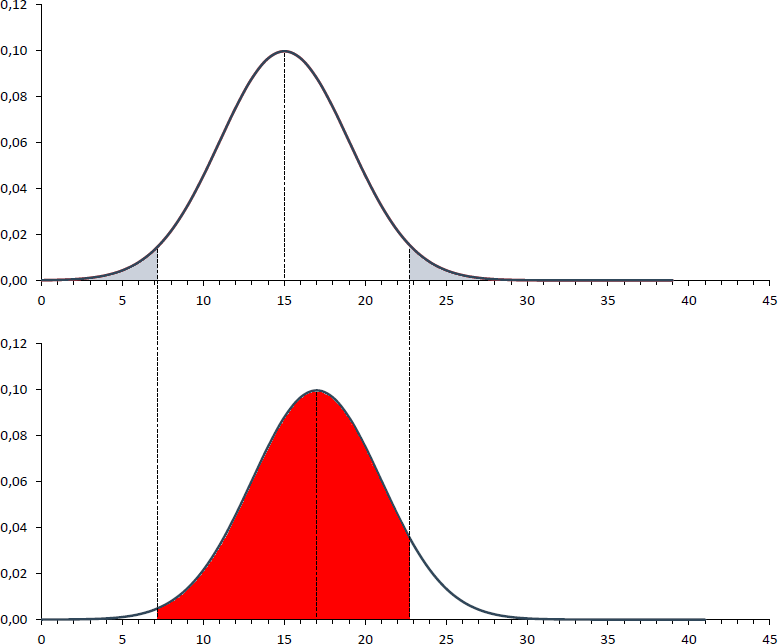
Die Wahrscheinlichkeit, mit der die falsche Nullhypothes nicht verworfen wird, hängt ihrerseits davon ab, wie hoch die Wahrscheinlichkeit ist, eine Stichproben mit einem Mittelwerten zwischen 7,2 und 22,8 Monaten zu ziehen, wenn die tatsächliche mittlere Karenzdauer 17 Monate beträgt.
Diese Wahrscheinlichkeit erhält man, indem zunächst bestimmt wird, mit welcher Wahrscheinlichkeit ein Mittelwert von 7,2 Monaten oder kleiner beobachtet wird und mit welcher Wahrscheinlichkeit ein Mittelwert von 22,8 Monaten oder kleiner beobachtet wird. Die Wahrscheinlichkeiten betragen 0,7% (z-Wert: -2,45) bzw. 92,6% (z-Wert: +1,45).
Damit beträgt die Wahrscheinlichkeit einen Mittelwert zwischen 7,2 und 22,8 Monaten zu beobachten und damit die Wahrscheinlichkeit eines β-Fehlers 91,9% (rote Fläche).