alpha-Fehler und beta-Fehler
Ein Hypothesentest besteht grob aus drei Teilen: (1) einer Annahme, welche Nullhypothese oder H0 genannt wird, (2) einer Beobachtung, die auf einer Stichprobe basiert, und (3) der Frage, wie wahrscheinlich es ist, gerade diese Beobachtung zu machen. Machen Sie sich dabei bitte bewusst: Die Frage können Sie nur auf Basis der Annahme beantworten.
Wenn Sie nun zum Schluss kommen, dass Ihre Beobachtung sehr unwahrscheinlich ist, haben Sie grundsätzlich zwei Möglichkeiten. (1) Sie glauben weiterhin, dass Ihre Annahme stimmt und Sie eben nur "Pech" hatten, oder (2) Sie verwerfen Ihre Nullhypothese, da es sich dabei ja "lediglich" um eine Annahme handelt und Sie eben nicht sicher sein können, dass diese stimmt. In der schließenden Statistik geht man ab einer bestimmten Grenze letzteren Weg, wobei die Grenze, ab wann etwas als zu unwahrscheinlich einzustufen ist, durch die (willkürliche) Wahl des Signifikanzniveaus gezogen wird. Dazu ein konkretes Beispiel.
Stellen Sie sich vor, Sie nehmen an, dass Frauen im Durchschnitt 15 Monate in Elternkarenz gehen. Das ist Ihre Nullhypothese. Basierend auf dieser Annahme bestimmen Sie, noch bevor Sie eine Stichprobe ziehen, welche Beobachtungen als zu unwahrscheinlich anzusehen sind, alsdass Sie weiterhin an der Nullhypothese festhalten wollen. Sagen wir, Sie ziehen diese Grenze bei 10%, was im Statistik-Jargon heißt, dass die Hypothese auf dem 10%-Niveau getestet wird. D.h. letztlich lediglich, dass Sie sich vorab entscheiden, Ihre Annahme immer dann zu verwerfen, wenn sie einen der 10%-unwahrscheinlichsten Fälle beobachten.
Nun ziehen Sie eine Stichprobe der Größe 500 und beobachten eine durchschnittliche Karenzdauer von 23 Monaten. Um die Grenzen gemessen in Monaten bestimmen zu können, ab denen die Annahme zu verwerfen ist, muss noch basierend auf der Stichprobe der Standardfehler geschätzt werden. Nehmen wir an dieser beträgt 4, womit die Grenzen (des Konfidenzintervalls) bei 7,2 bzw. 22,8 Monaten liegen. Da die Beobachtung außerhalb dieser Grenzen liegt, die den Bereich der 10% der unwahrscheinlichsten Fälle abgrenzt, verwerfen Sie die Nullhypothese.
α-Fehler
Damit kann es aber passieren, dass eine richtige Nullhypothese verworfen wird, nur weil man das Pech hatte eine sehr unwahrscheinliche Beobachtung zu machen. Dieser Fehler wird α-Fehler (oder Fehler 1. Art, Type-I-Fehler oder Irrtumswahrscheinlichkeit) genannt und entspricht dem Signifikanzniveau.
Daraus folgt aber: Je kleiner das Signifikanzniveau, desto kleiner die Wahrscheinlichkeit, einen α-Fehler zu begehen und damit eine richtige Nullhypothese H0 zu verwerfen. Die farbigen Flächen in nachfolgender Abbildung stehen für diese Wahrscheinlichkeit.
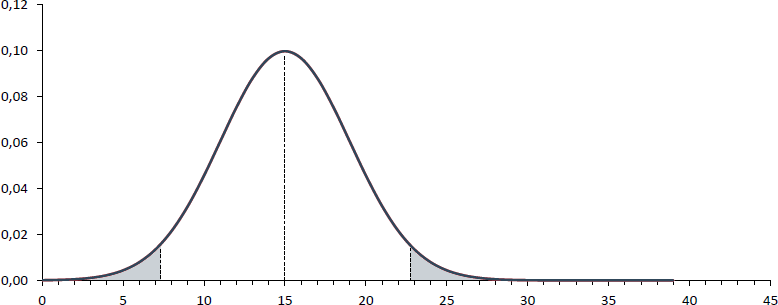
Um diese Wahrscheinlichkeit zu reduzieren, könnte man auf die Idee kommen, ein möglichst kleines Signifikanzniveau zu wählen, da dadurch die Wahrscheinlichkeit eines α-Fehlers sinkt. Welcher Nachteil damit einhergeht, zeigt die nächste Abbildung.
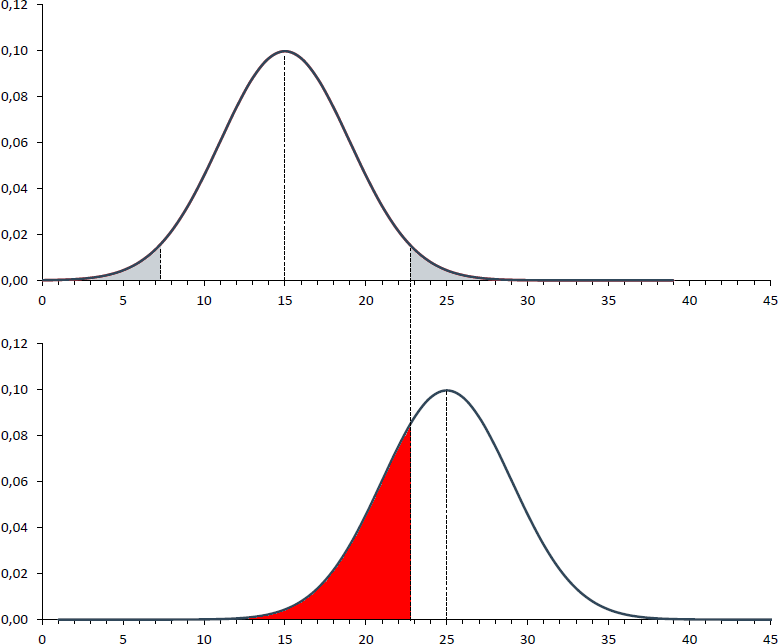
β-Fehler
Um beim Beispiel zu bleiben: Stellen Sie sich vor, dass Frauen in Wahrheit im Durchschnitt tatsächlich 25 Monate in Elternkarenz gehen und damit die untere Verteilung die richtige, die "wahre" ist.
Da eine beobachtete (mittlere) Karenzdauer von unter 22,8 Monaten dazu führt, dass die falsche Nullhypothese nicht verworfen wird, kann man sich ausrechnen, wie hoch die Wahrscheinlichkeit ist, bei einer tatsächlichen durchschnittlichen Karenzdauer von 25 Monaten eine Stichprobe zu ziehen und dabei eine Karenzdauer von 22,8 Monaten oder kleiner zu erhalten [1]. Diese Wahrscheinlichkeit beträgt 29,1% (z-Wert: -0,55) und entspricht der rot gefärbten Fläche.
D.h., mit einer Wahrscheinlichkeit von 29,1% zieht man eine Stichprobe, die dazu führt, dass eine falsche H0 nicht verworfen wird. Dieser Fehler wird β-Fehler (oder Fehler 2. Art oder Type-II-Fehler) genannt.
Wird nun das Signifikanzniveau erhöht, so sinkt dadurch zwar die Wahrscheinlichkeit einen α-Fehler zu begehen (farbige Fläche im oberen Teil der folgenden Abbildung), aber gleichzeitig steigt die Wahrscheinlichkeit für einen β-Fehler (rote Fläche im unteren Teil).
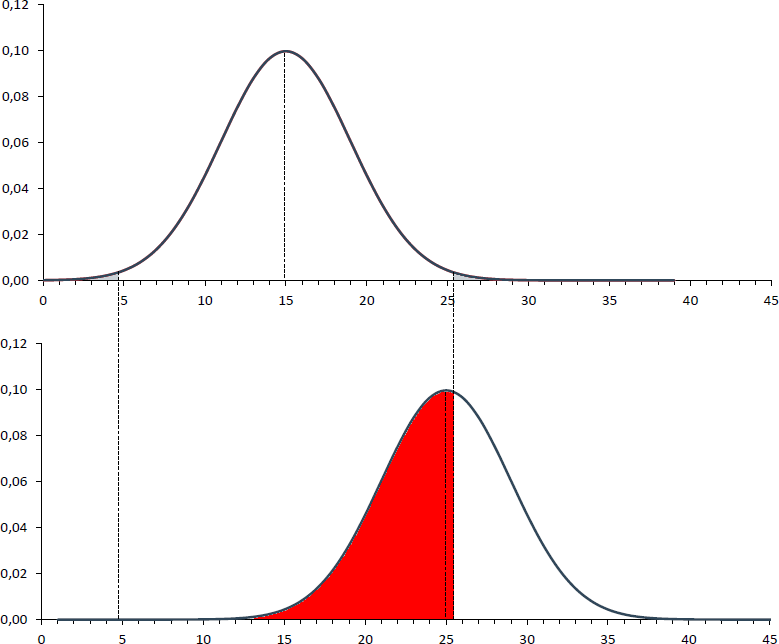
Da der β-Fehler seinerseits unter anderem von der Lage der "wahren" Verteilung abhängt und diese unbekannt ist, kennt man in der Praxis die Wahrscheinlichkeit einen β-Fehler zu begehen nicht. Daher wird gelegentlich berechnet, mit welcher Wahrscheinlichkeit eine falsche H0 auch tatsächlich verworfen wird. Aber das ist ein anderes Thema, welches unter dem Begriff Power besprochen wird.
Hier finden Sie ein weiteres Beispiel zur Berechnung der β-Fehler-Wahrscheinlichkeit.
[1] Etwas genauer gesagt, entspricht der β-Fehler der Fläche zwischen 7,2 und 22,8 Monaten. Da jedoch die Wahrscheinlichkeit mit der bei einer wahren durchschnittlichen Karenzdauer von 25 Monaten, eine Stichprobe mit einer mittleren Karenzdauer von 7,2 Monaten oder geringer gezogen wird, praktisch Null ist, ist die Wahrscheinlichkeit eine mittlere Karenzdauer kleiner 22,8 Monate zu beobachten gleich der Wahrscheinlichkeit, eine mittlere Karenzdauer zwischen 7,2 und 22,8 Monaten zu beobachten.