Die χ2-Verteilung
Ähnlich wie die t-Verteilung hängt auch die Form der χ2-Verteilung von der Anzahl an Freiheitsgraden ab. χ2-Verteilungen leiten sich dabei von Standardnormalverteilungen ab. Konkret ist die χ2-Verteilung die Summe aus quadrierten standardnormalverteilten Variablen, wobei die Anzahl an Summanden die Anzahl an Freiheitsgraden der χ2-Verteilung bestimmt.
Aus der Tatsache, dass es sich bei der χ2-Verteilung um das Quadrat von standardnormalverteilten Variablen handelt, folgt, dass χ2-Werte immer positiv sind. Nachfolgende Abbildung zeigt exemplarisch zwei Beispiele für χ2-Verteilungen mit unterschiedlichen Freiheitsgraden.
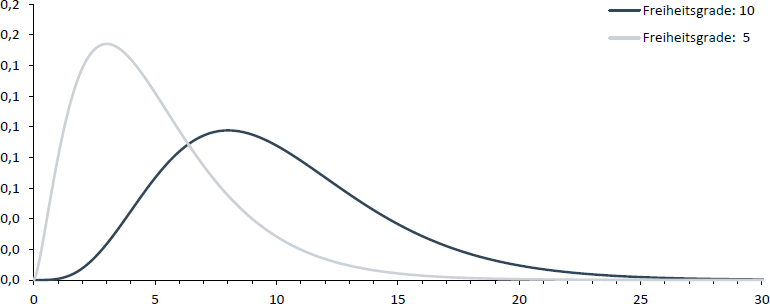
Beispiel
Stellen Sie sich vor, Sie möchten jenen χ2-Wert bestimmen, von dem links 90% der Fläche liegen (farbige Fläche in der folgenden Abbildung). Die Anzahl an Freiheitsgraden sei 10.
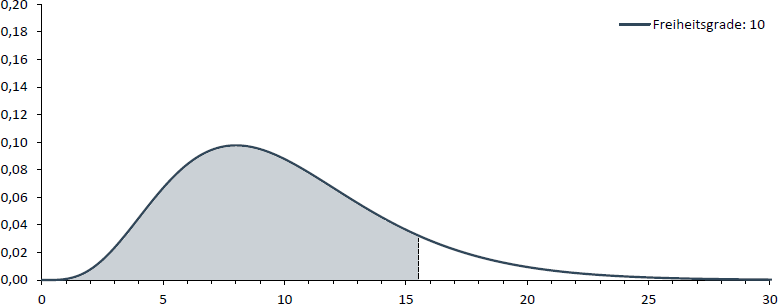
Die Tabelle, der Sie den entsprechenden χ2-Wert entnehmen können, ist derart aufgebaut, dass Sie in der ersten Zeile ausgewählte Flächen finden und in der ersten Spalte die Anzahl an Freiheitsgraden. Dort, wo sich die Zeile mit der Spalte kreuzt, können Sie den gesuchten χ2-Wert finden. Dieser beträgt im Beispiel 15,987.
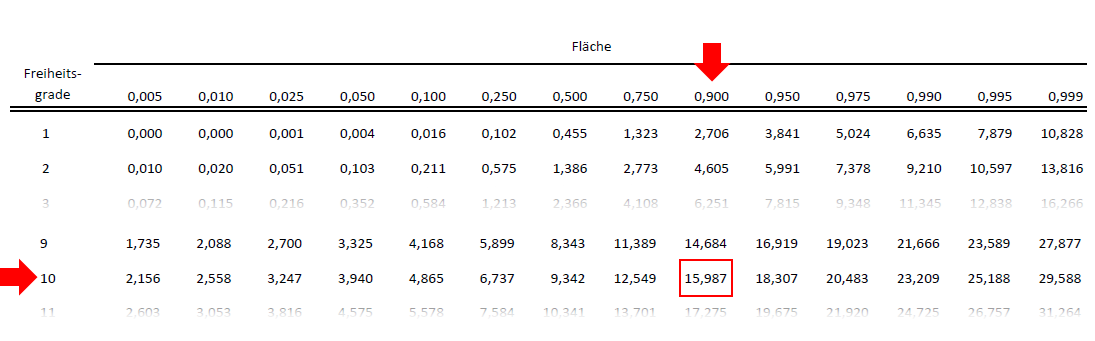
D.h., die Wahrscheinlichkeit bei df = 10 einen χ2-Wert kleiner (gleich) 15,987 zu beobachten, beträgt 90%.
Da sich die grundsätzliche Interpretation der χ2-Werte nicht von jener der z-Wert unterscheidet, wird für weitere Beispiele auf der Seite "Standardnormalverteilung" verwiesen.