Wie die Verteilungen zusammenhängen
In aller Kürze wird gezeigt, wie die
- Binomialverteilung
- Normalverteilung
- Standardnormalverteilung
- χ2-Verteilung
- t-Verteilung
- F-Verteilung
zusammenhängen.
Binomialverteilung
Die Binomialverteilung zählt zu den wichtigsten diskreten Verteilungen. Im Rahmen der Binomialverteilung betrachten wir eine Zufallsvariable, die lediglich zwei Ereignisse kennt, wobei es egal ist, ob die beiden Ereignisse mit gleicher Wahrscheinlichkeit eintreten oder nicht.
Klassisches Beispiel ist der Münzwurf. Die beiden (gleichwahrscheinlichen) Ereignisse sind dabei Kopf und Zahl. Ein anderes Beispiel ist die Zufallsvariable "Gerades Ergebnis beim Wurf eines Würfels", wobei die beiden Ereignisse wieder mit gleicher Wahrscheinlichkeit eintreten.
Beispiele, bei denen die Ereignisse mit ungleicher Wahrscheinlichkeit eintreten sind "Zahl 6 beim Wurf eines Würfels", oder Stadtkind versus Landkind, Raucher versus Nichtraucher etc.
Die weiteren Ausführen seien an einem konkreten Beispiel festgemacht. Stellen Sie sich vor, wir werfen eine Münze und zählen immer wie oft Kopf gefallen ist. Wenn wir annehmen, dass die Münze nie auf der Kante stehen bleiben kann, dann treten die beiden Ereignisse Kopf und Zahl jeweils mit einer Wahrscheinlichkeit von 50% ein. Wird nun die Münze lediglich einmal geworfen, so verteilt sich die Wahrscheinlichkeit null Mal Kopf bzw. einmal Kopf zu beobachten, wie in der folgenden Abbildung dargestellt.
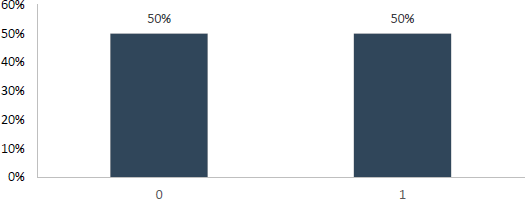
Wird die Münze 2-mal geworfen, treten 0-mal (25%), 1-mal (50%) bzw. 2-mal (25%) Kopf wie in der folgenden Abbildung auf. Bereits in dieser Abbildung kann man erkennen, dass sich die Form der Verteilung leicht hin zu einer Glockenform verändert hat.
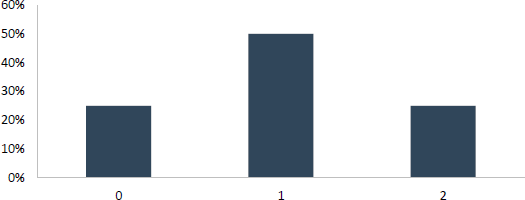
Wird die Münze 20-mal geworfen, dann können wir wieder grafisch darstellen (folgende Abbildung), mit welcher Wahrscheinlichkeit eine bestimmte Anzahl an Köpfen beobachtet wird.
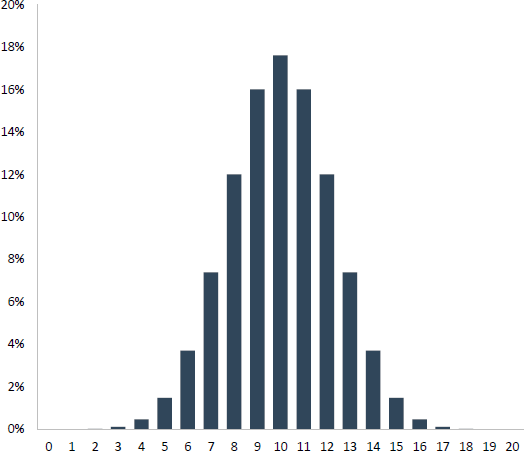
Bereits diese wenigen Abbildungen machen deutlich, dass sich die Binomialverteilung mit einer steigenden Anzahl an Münzwürfen mehr und mehr einer Glockenform annähert. Die Anzahl an Münzwürfen steht dabei für nichts anderes als die Stichprobengröße, und es kann mathematisch bewiesen werden, dass die Binomialverteilung perfekt mit der Normalverteilung übereinstimmt, wenn wir unendlich oft die Münze unendlich oft werfen würden (also unendlich viele Stichproben vorliegen, die unendlich groß sind). Man sagt, die Binomialverteilung geht in eine Normalverteilung über.
Normalverteilung
Jede Normalverteilung kann durch die Formel
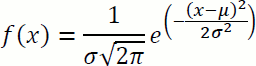
beschrieben werden.
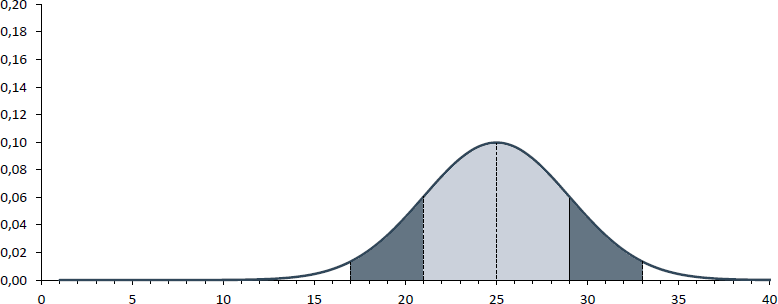
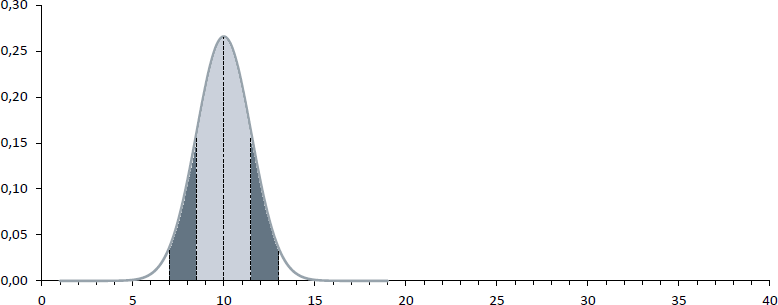
Normalverteilungen unterscheiden sich dabei einzig und alleine durch ihr Zentrum µ und die Streuung σ. Die beiden nachfolgenden Abbildungen zeigen Normalverteilungen mit µ = 25 bzw. 10 und σ = 4 bzw. 1,5. Unabhängig von der konkreten Form der Normalverteilung gilt aber immer, dass sich im Intervall [µ - σ; µ + σ] rund 68% (helle Flächen) und im Intervall [µ - 2σ; µ + 2σ] rund 95,5% (helle + dunkle Flächen) aller Fälle liegen.
Die Intervalle für die nachfolgende Abbildung lauten konkret: [21; 29] bzw. [17; 33].
Die Intervalle für die nachfolgende Abbildung lauten konkret: [8,5; 11,5] bzw. [7; 13].
Auch gilt immer, dass jede Normalverteilung durch

in eine Standardnormalverteilung transformiert werden kann (z-Transformation).
Standardnormalverteilung
Der große Vorteil der Standardnormalverteilung ist, dass die Flächen für ausgewählte z-Werte in Tabellen publiziert werden und nicht jedes Mal auf's Neue berechnen werden müssen.

χ2-Verteilung
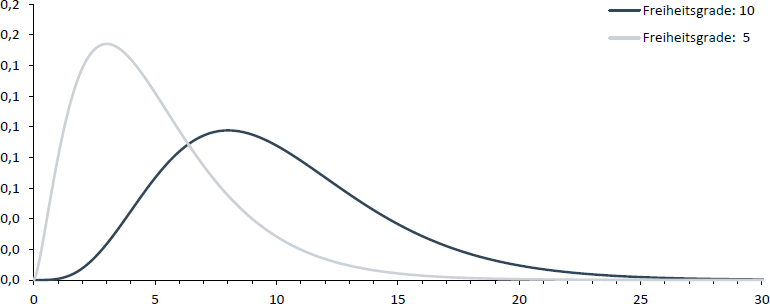
Wird eine standardnormalverteilte Variable quadriert - wie dies bspw. bei der Berechnung der Varianz der Fall ist -, so erhält man eine χ2-verteilte Variable.
χ2-verteilte Variablen können dabei aus mehreren quadrierten standardnormalverteilten Variablen zusammengesetzt sein, was in der Anzahl an Freiheitsgraden zum Ausdruck kommt. Diese bestimmen letztlich auch die genaue Form der χ2-Verteilung.
t-Verteilung
Muss bei der z-Transformation die Streuung der Grundgesamtheit geschätzt werden, so ergibt dies auf Grund dessen, dass der Zähler eine normalverteilte Variable enthält und der Nenner eine χ2-verteilte, eine t-verteilte Variable. Da dabei die χ2-verteilte Variable von der Anzahl an Freiheitsgraden abhängt, tut dies auch die t-verteilte Variable.
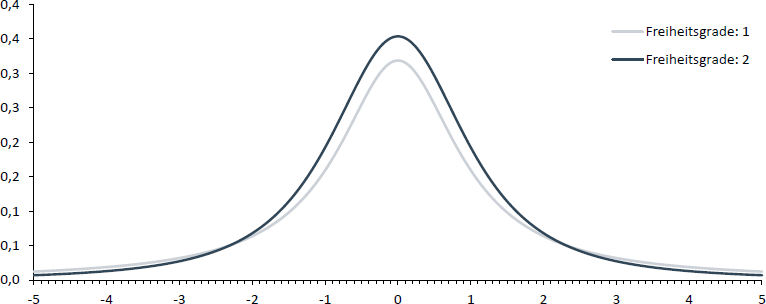
Wie für die Binomialverteilung gilt auch für die t-Verteilung, dass sie sich mit steigendem Stichprobenumfang der Normalverteilung annähert.
F-Verteilung
Wird das Verhältnis von zwei χ2-verteilten Variablen gebildet, wie dies bspw. beim sog. F-Test auf Varianzhomogenität der Fall ist, so erhält man eine F-verteilte Variable.
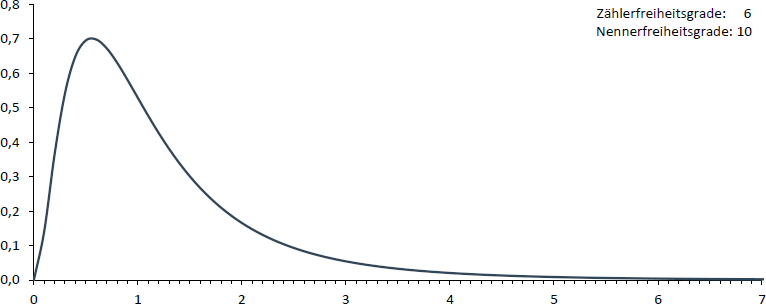
Da nun sowohl der Zähler als auch der Nenner eine χ2-verteilte Variable enthält und die Form der jeweiligen χ2-Verteilung von der Anzahl an Freiheitsgraden abhängt, hängt die F-Verteilung sowohl von der Anzahl an Freiheitsgraden im Zähler als auch der Anzahl an Freiheitsgraden im Nenner ab.