Die t-Verteilung
Da sich die grundsätzliche Interpretation der t-Werte nicht von jener der z-Werte unterscheidet, wird auf die Beispiele auf der Seite "Standardnormalverteilung" verwiesen.
Stattdessen wird ein wesentlicher Unterschied, der zwischen den beiden Verteilungen besteht, herausgearbeitet. Dieser Unterschied besteht darin, dass die Form der t-Verteilung von der Stichprobengröße bzw. der Anzahl an Freiheitsgraden abhängt. Aus dieser Eigenschaft folgt auch die etwas andere Darstellung in der Tabelle.
Damit wird folgenden Fragen nachgegangen:
- Frage 1: Was kann man sich unter Freiheitsgraden vorstellen?
- Frage 2: Wie ist die t-Verteilungs-Tabelle zu lesen?
Was kann man sich unter Freiheitsgraden vorstellen?
Das Prinzip ist rasch an einem Beispiel illustriert:
Stellen Sie sich vor das arithmetische Mittel aus drei Zahlen beträgt 15. Das bedeutet, dass grundsätzlich nachfolgende Gleichung erfüllt sein muss:
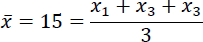
Wie viele der x-Werte können Sie frei wählen, sodass "am Ende" 15 herauskommt? Richtig, immer nur 2. Sie können zwar beliebige Wert für x1 und x2, x1 und x2 bzw. x2 und x3 wählen, aber der letzte x-Wert kann nicht mehr frei gewählt werden, weil es die Restriktion gibt, dass als arithmetisches Mittel 15 herauskommen muss.
Damit gibt es in diesem Beispiel 2 Freiheitsgrade, was kurz mit df = 2 (degrees of freedom) geschrieben wird.Die Anzahl an Freiheitsgraden df entspricht der Stichprobengröße minus 1, also df = n - 1.
Wie ist die t-Verteilungs-Tabelle zu lesen?
Wie die nachfolgende Abbildung zeigt, ändert sich die Form der t-Verteilung in Abhängigkeit von der Anzahl an Freiheitsgraden, weshalb die Fläche, die bspw. links von einem t-Wert von 1 liegt, bei df = 1 und df = 2 deutlich unterschiedlich ist.
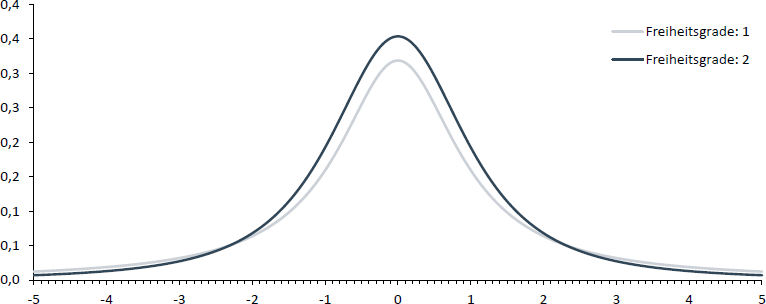
Da dies der Fall ist, erfolgt die Darstellung in der Tabelle der t-Verteilung nicht analog zur Darstellung in der Standardnormalverteilungs-Tabelle.
Vielmehr wird in Abhängigkeit von der Anzahl an Freiheitsgraden für bestimmte Flächen der jeweilige t-Wert ausgewiesen. Nachfolgender Ausschnitt aus der t-Verteilungs-Tabelle veranschaulicht das Prinzip
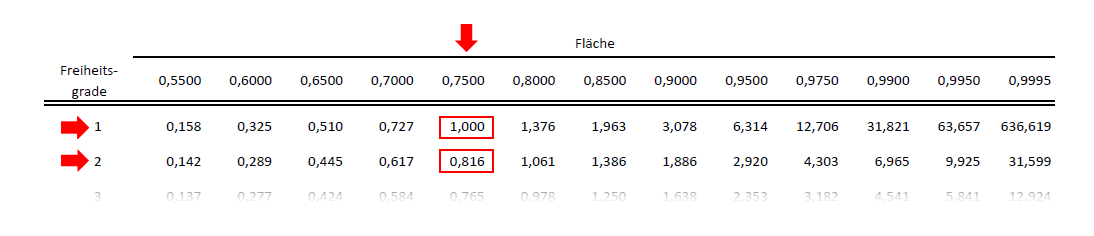
Wenn df = 1 ist und damit die helle t-Verteilung gilt, liegen 75% der Fläche links von einem t-Wert von 1. Damit liegen 25% rechts von einem t-Wert von 1.
Wie der Abbildung entnommen werden kann, liegt die t-Verteilung (im Zentrum) mit df = 1 unterhalb der t-Verteilung mit df = 2. Dies hat zur Folge, dass der t-Wert, von dem links 75% der Fläche liegen, bei df = 2 kleiner ist. Er beträgt für df = 2 0,816.