Wann die t-Verteilung verwendet wird
Unverbundene Stichproben
Auf der Seite "Woher kommt die Bedeutung der Normalverteilung" wird an Hand eines Merkmals, das selbst nicht normalverteilt ist, gezeigt, dass bei Ziehung unendlich vieler Stichproben die unendlich vielen Mittelwerte selbst normalverteilt sind.
Das gewählte Beispiel sollte dabei letztlich ein sehr allgemeines Ergebnis illustrieren, nämlich, dass unter bestimmten und wenig restriktiven Annahmen die Verteilung des Mittelwertes (mit wenigen Ausnahmen) unabhängig von der Verteilung in der Grundgesamtheit ist, weil dieser (fast) immer einer Normalverteilung folgt.
Auf der Seite "Warum die Standardnormalverteilung praktisch ist" wird gezeigt, dass jede Normalverteilung durch eine sogenannte z-Transformation in eine Standardnormalverteilung transformiert werden kann und diese Tatsache uns das Berechnen von Wahrscheinlichkeiten erspart, weil die Werte einer Tabelle entnommen werden können.
Die Formel, mit der die z-Transformation durchgeführt wird, sieht dabei wie folgt aus:
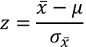
Der µ-Wert im Zähler steht dabei für den "Mittelwert der Grundgesamtheit" und ist eine feste Zahl, genau so wie der Standardfehler. Lediglich der Mittelwert ist eine Zufallsvariable, von der wir wissen, dass dieser normalverteilt ist. D.h., einzig der Mittelwert der Stichprobe ist keine feste Zahl, weshalb die z-Werte derselben Verteilung folgen wie der Mittelwert. Beide sind normalverteilt.
Die Höhe des Standardfehlers wiederum hängt zum einen von der Größe der Stichproben und zum anderen von der Streuung in der Grundgesamtheit σ ab und wird wie folgt berechnet:
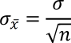
In der Praxis ist aber die Streuung in der Grundgesamtheit häufig unbekannt, weshalb diese auf Basis der Stichprobe über
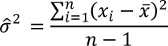
geschätzt werden muss.
Da aber die Stichprobe zufällig gezogen ist, ist auch das Schätzergebnis für die Streuung der Grundgesamtheit zufällig - und folgt damit selbst einer bestimmten Verteilung. Zur Berechnung des Standardfehlers wiederum wird diese Zufallsvariable durch n0,5 und damit durch eine feste Zahl dividiert. Daher folgt der (geschätzte) Standardfehler derselben Verteilung wie die (geschätzte) Streuung der Grundgesamtheit. Beide sind χ2-verteilt.
Da es sich nun um Schätzungen handelt, wird dies auch in der Notation zum Ausdruck gebracht und sieht wie folgt aus:
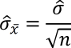
Und das ist in unserem Zusammenhang der springende Punkt.
Muss die Streuung der Grundgesamtheit geschätzt werden, wird der Standardfehler zur Zufallsvariable. Bei der z-Transformation taucht damit aber sowohl im Zähler als auch im Nenner eine Zufallsvariable auf und das Ergebnis - der "z-Wert" - folgt dadurch einer anderen, einer neuen Verteilung. Diese wird nun t-Verteilung genannt und die dazugehörenden Werte heissen logischerweise t-Werte. Die Form der t-Verteilung hängt dabei von der Stichprobengröße, den sog. Freiheitsgraden, ab.
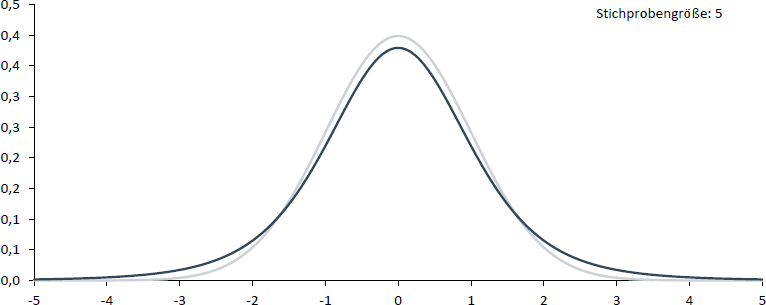
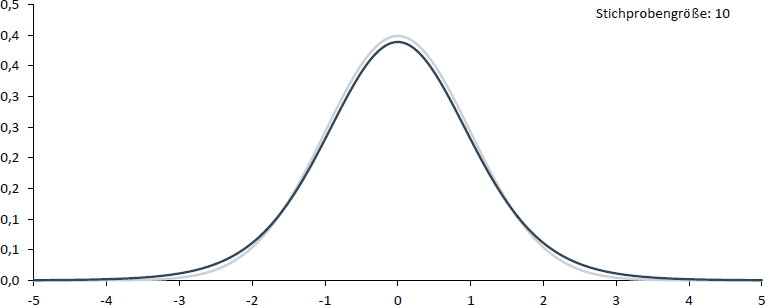
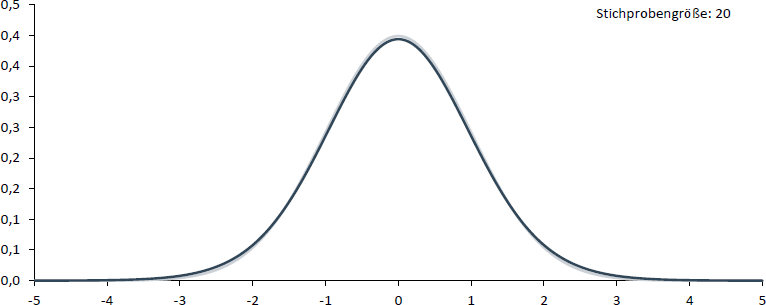
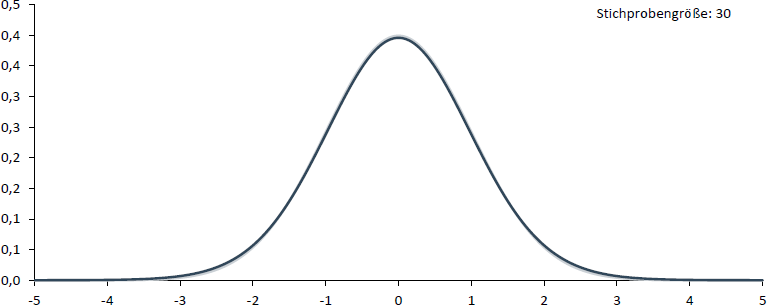
Dass eine Unterscheidung zwischen Normalverteilung und t-Verteilung in der Praxis jedoch lediglich für kleine Stichproben von Bedeutung ist, zeigen die folgenden vier Abbildungen, in denen die t-Verteilung (dunkel) der Standardnormalverteilung (hell) gegenübergestellt wird. Wie Sie sehen können, spielt eine Unterscheidung ab einer Stichprobengröße von 30 kaum noch eine Rolle.
Die ganze Diskussion ist damit vor allem eine Erklärung dafür, warum im Output von Statistikprogrammen manchmal t-Werte zu finden sind und keine z-Werte.
(Klicken Sie mit der rechten Maustaste auf die Grafik um die Grafik vergrößert anzeigen zu lassen.)