Die Standardnormalverteilung
Unverbundene Stichproben
Im Folgenden wird anhand von vier Fragen die Verwendung der Standardnormalverteilungs-Tabelle erläutert. Die Fragen lauten:
- Frage 1: Wie hoch ist die Wahrscheinlichkeit, einen z-Wert von 1,25 oder kleiner zu beobachten?
- Frage 2: Wie hoch ist die Wahrscheinlichkeit, einen z-Wert von 0,67 oder höher zu beobachten?
- Frage 3: Wie hoch ist die Wahrscheinlichkeit, einen z-Wert von -0,67 oder kleiner zu beobachten?
- Frage 4: Wie hoch ist die Wahrscheinlichkeit, einen z-Wert zwischen 0,67 und 1,25 zu beobachten?
Zur Beantwortung der Fragen, muss folgendes bekannt sein:
- Die Fläche unter der Standardnormalverteilung entspricht 100%.
- Die Standardnormalverteilungs-Tabelle gibt immer die Fläche an, die links vom jeweiligen z-Wert liegt.
- Damit errechnet sich die Fläche rechts von einem z-Wert über die Berechnung der Restfläche, die auf 100% fehlt.
Frage 1
Wenn die Frage beantwortet werden soll, wie hoch die Wahrscheinlichkeit ist, einen z-Wert von 1,25 oder kleiner zu beobachten, so ist die farbige Fläche in der nachfolgenden Abbildung gesucht.
Der z-Wert kann der Standardnormalverteilungs-Tabelle wie angezeigt entnommen werden. Der ersten Spalte ist dabei die Einerstelle zusammen mit der ersten Dezimalstelle des z-Wertes zu entnehmen. In der ersten Zeile finden Sie die zweite Dezimalstelle des z-Wertes. Dort, wo sich die jeweilige Zeile mit der jeweiligen Spalte kreuzt, finden Sie die Wahrscheinlichkeit, den jeweiligen z-Wert oder einen kleineren zu beobachten.
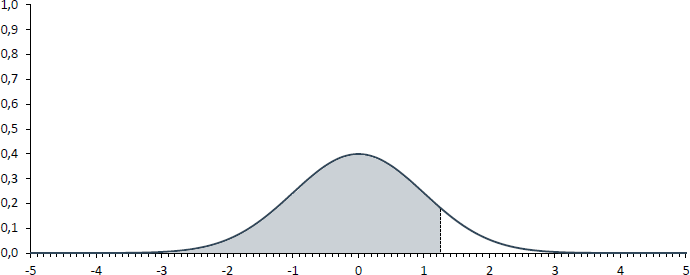
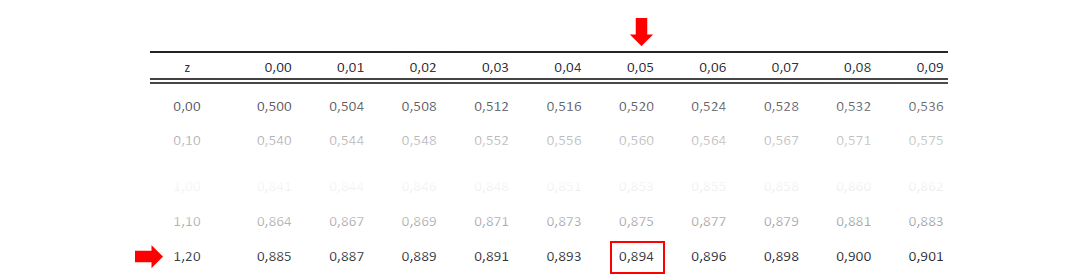
Damit beträgt die Wahrscheinlichkeit, einen z-Wert von 1,25 oder kleiner zu beobachten, 89,4%.
Frage 2
Wenn die Frage beantwortet werden soll, wie hoch die Wahrscheinlichkeit ist, einen z-Wert von 0,67 oder größer zu beobachten, so ist die farbige Fläche in der nachfolgenden Abbildung gesucht.
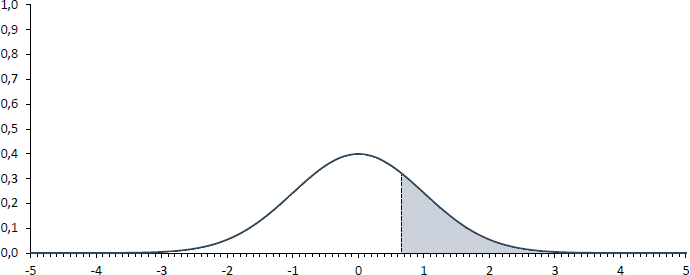
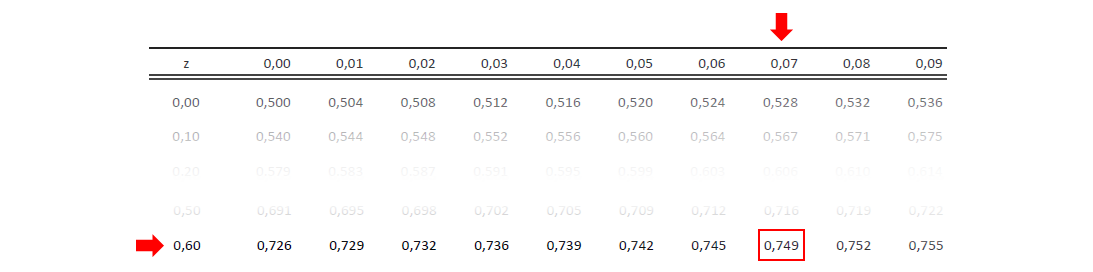
Die Wahrscheinlichkeit, die der Standardnormalverteilungs-Tabelle für einen z-Wert von 0,67 entnommen werden kann, entspricht jedoch der weißen Fläche in obiger Abbildung, also der Fläche links von 0,67 und beträgt 74,9%. Da die Fläche unter der Standardnormalverteilung jedoch immer 100% entspricht, kann die Fläche rechts von 0,67 über 100% - 74,9% berechnet werden und beträgt 25,1%.
Frage 3
Wenn die Frage beantwortet werden soll, wie hoch die Wahrscheinlichkeit ist, einen z-Wert von -0,67 oder kleiner zu beobachten, so ist die farbige Fläche in der nachfolgenden Abbildung gesucht.
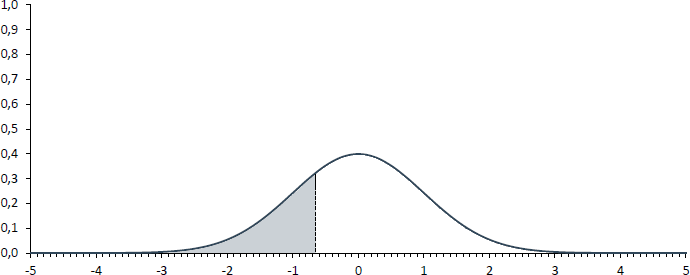
In der Standardnormalverteilungs-Tabelle sind jedoch keine negativen z-Wert zu finden. Dies ist aber auch nicht notwendig, weil die Verteilung symmetrisch ist und daher die Fläche links von 0,67 genau so groß ist wie die Fläche rechts von -0,67 (vgl. dazu die Abbildung unter Frage 2). Damit kann die Frage beantwortet werden, indem der Tabelle die Wahrscheinlichkeit für einen z-Wert von höchstens 0,67 entnommen wird, welche 74,9% beträgt. Die gesuchte Wahrscheinlichkeit beträgt 100% - 74,9% und damit 25,1%.

Frage 4
Wenn die Frage beantwortet werden soll, wie hoch die Wahrscheinlichkeit ist, einen z-Wert zwischen 0,67 und 1,25 zu beobachten, so ist die farbige Fläche in der nachfolgenden Abbildung gesucht.
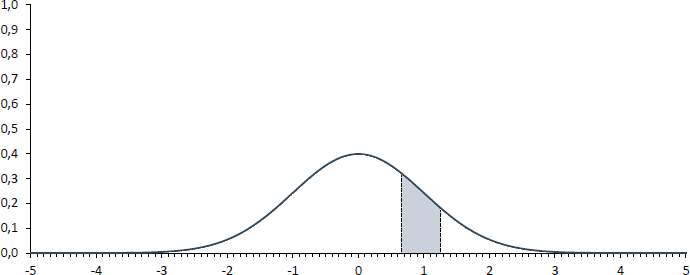
Da die Wahrscheinlichkeit, einen z-Wert keiner 1,25 zu beobachten, 89,4% (Frage 1), die Wahrscheinlichkeit, einen z-Wert kleiner 0,67 zu beobachten 74,9% (Frage 2) und die Gesamtfläche 100% beträgt, errechnet sich die gesuchte Wahrscheinlichkeit via 89,4% - 74,9% und beträgt damit 14,5%.