Warum die Standardnormalverteilung praktisch ist
In der nachfolgenden Abbildung finden Sie zwei Beispiele für normalverteilte Grundgesamtheiten. Um es konkreter zu machen, stellen wir uns vor, es handelt sich in der linken oberen Abbildung um das Alter, mit dem Jugendliche das erste Mal mit Alkohol in Berührung kommen. Der µ-Wert von 14 besagt in dem Fall, dass dies im Mittel mit 14 Jahren der Fall ist.
In der rechten (oberen) Grundgesamtheit sind der µ-Wert sowie die Streuung σ etwas größer, weshalb die Verteilung im Vergleich zur linken weiter rechts liegt und flacher verläuft. Die Interpretation ist ansonsten analog.
Stellen Sie sich nun vor, Sie ziehen aus der linken Grundgesamtheit unendlich viele Stichproben der Größe 50 und berechnen als Kennwert der Stichprobe jeweils den Mittelwert. Es dürfte klar sein, dass dabei nicht immer derselbe Mittelwert herauskommt. Weniger offensichtlich ist vielleicht, dass die Mittelwerte selbst wieder normalverteilt sind - genauso wie das Merkmal "Alter" in der Grundgesamtheit.
Die Mittelwerte streuen aber deutlich weniger, weshalb die Verteilung der Mittelwerte, welche auch Stichprobenkennwertverteilung genannt wird, spitzer und damit höher wird. Die beiden Stichprobenkennwertverteilungen sind im unteren Teil der Abbildung dargestellt.
Wenn die Streuuung der Grundgesamtheit bekannt ist, kann die Streuung der Stichprobenkennwertverteilung mit folgender Formel berechnet werden:
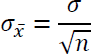
Beachten Sie, dass das Streuungsmaß, das die Streuung der Grundgesamtheit beschreibt, Standardabweichung genannt wird und jenes, das die Streuung des Stichprobenkennwertes beschreibt Standardfehler. Beachten Sie ferner, dass der Mittelwert des durchschnittlichen Alters (unterer Teil) ident ist mit dem Mittelwert des Alters in der Grundgesamtheit (oberer Teil).
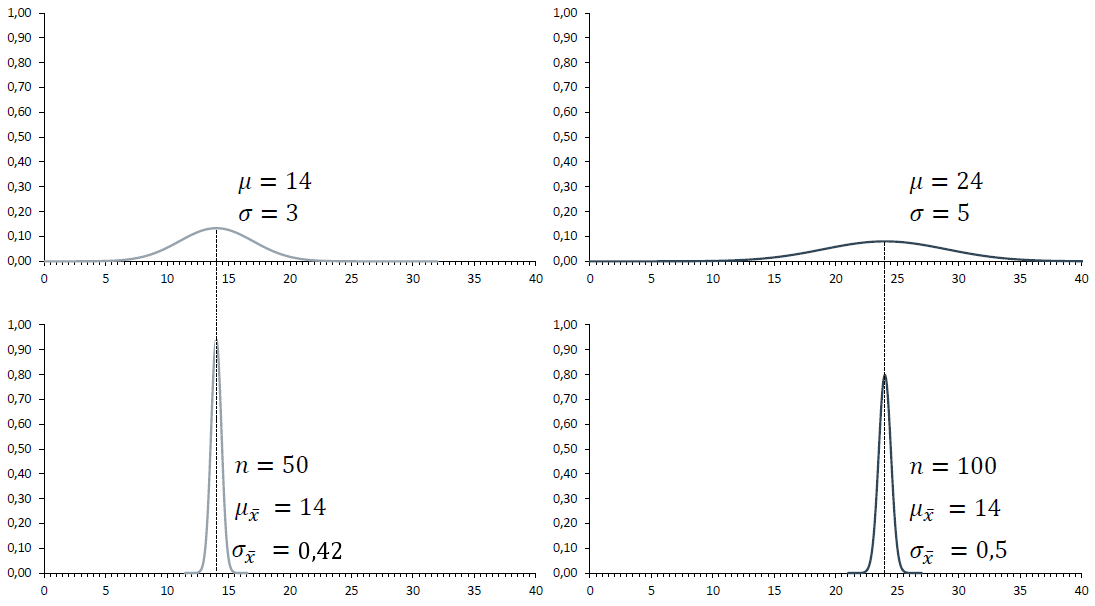
Man könnte sich nun die Frage stellen, wie hoch die Wahrscheinlichkeit ist, eine Stichprobe aus einer Grundgesamtheit mit µ = 14 Jahre und σ = 3 Jahren zu ziehen und dabei einen Mittelwert von 15 Jahren oder größer zu erhalten. Oder für die rechte Grundgesamtheit könnte man sich die Frage stellen, wie hoch die Wahrscheinlichkeit ist, eine Stichprobe zu ziehen und einen Mittelwert größer 25 oder kleiner 23 zu erhalten. In beiden Fällen bedeutet das, dass wir an den Flächen interessiert sind, die in der nächsten Abbildung rot eingefärbt sind und die jeweilige Stichprobenkennwertverteilung vergrößert zeigen.
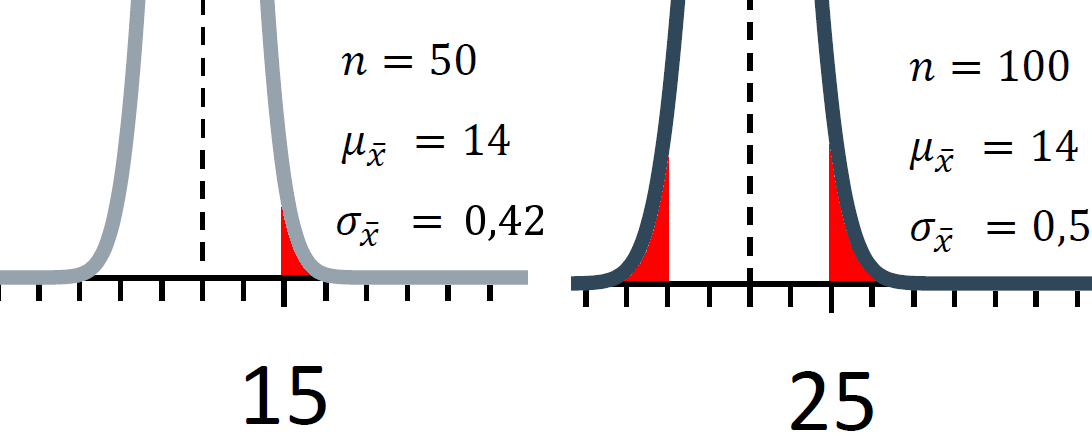
Da es sich in beiden Fällen um eine Normalverteilung handelt und diese durch die Formel
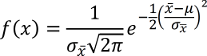
beschrieben wird, könnte man "einfach" das entsprechende Integral bilden um die Flächen zu erhalten.
Das wäre aber mühsam und vor allem: Immer wenn die Fragestellung auch nur mininal geändert wird oder die Parameter der Grundgesamtheit andere sind, müsste jedes Mal auf's Neue das entsprechende Integral berechnet werden.
Um das zu umgehen, kann alternativ jeder einzelne Mittelwert durch Anwendung der Formel
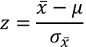
in sogenannte z-Werte transformiert werden (z-Transformation). Diese z-Werte sind immer standardnormalverteilt, was bedeutet, dass diese Verteilung immer die Werte µ = 0 und σ = 1 hat und damit immer gleich aussieht.
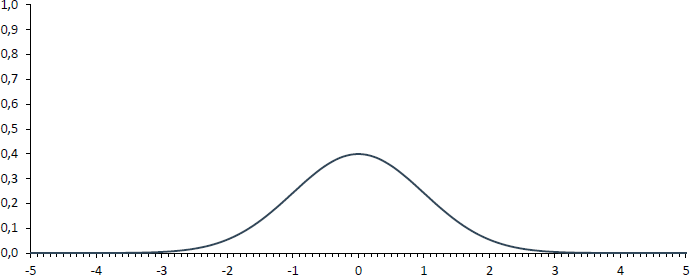
Weil dieser Vorgang aber immer zur Standardnormalverteilung führt, macht es auch Sinn, die Flächen, die links vom jeweiligen z-Wert liegen, in einer Tabelle zu publizieren. Die Werte sind als Wahrscheinlichkeiten zu interpretieren mit der bspw. ein z-Wert von 1,25 oder kleiner, -1 [1] oder kleiner oder sonst irgendein Wert beobachtet wird (nachfolgende Abbildungen veranschaulichen dies graphisch).
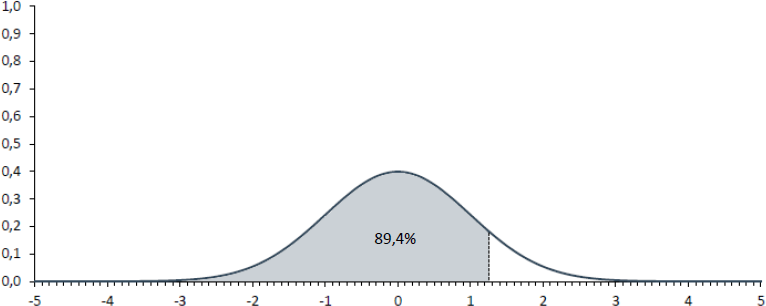
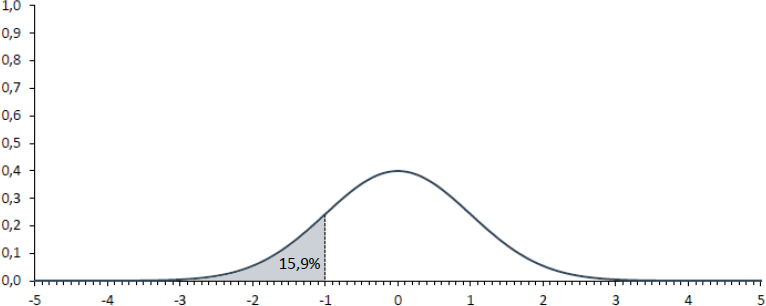
Im Beispiel mit dem Alter ergibt sich übrigens ein z-Wert von 2,38 [2]. Die Wahrscheinlichkeit, diesen z-Wert oder einen kleineren zu beobachten - und das ist das gleiche wie zu fragen, wie hoch die Wahrscheinlichkeit ist in einer Zufallsstichprobe ein durchschnittliches Alter von 15 Jahren oder jünger zu erhalten - kann nun ganz einfach der Standardnormalverteilungs-Tabelle entnommen werden und beträgt 99,1%. Damit beträgt die Wahrscheinlichkeit, einen z-Wert von größer 2,38 zu beobachten, 0,9%.
Im rechten Beispiel ist der z-Wert, der mit einem Mittelwert von 25 bzw. 23 korrespondiert, +2 bzw. -2 [3], wobei die Wahrscheinlichkeit, einen z-Wert von +2 oder kleiner zu beobachten, 97,7% beträgt. Die Wahrscheinlichkeit einen z-Wert von +2 oder höher zu beobachten, beträgt dementsprechend 2,3%. Da die Verteilung symmetrisch ist, ist die Wahrscheinlichkeit, einen z-Wert von +2 oder höher zu beobachten, gleich der Wahrscheinlichkeit, einen z-Wert von -2 oder kleiner zu beobachten. Daher beträgt die Wahrscheinlichkeit einen Mittelwert kleiner (gleich) 23 oder größer (gleich) 25 zu beobachten 4,6%.
Zusammenfassung Jede Normalverteilung kann durch eine sogenannte z-Transformation in eine Standardnormalverteilung transformiert werden. Das hat den Vorteil, dass die Wahrscheinlichkeiten für ausgewählte z-Werte einer Tabelle entnommen werden können und nicht jedes Mal auf's Neue berechnet werden müssen.
[1] Die Tabelle weist ausschließlich die Wahrscheinlichkeiten für positive z-Werte aus, da auf Grund der Symmetrie die Fläche für negative z-Werte über "1-Fläche(positiver z-Wert)" berechnet werden kann. Im konkreten Fall beträgt die Fläche links von +1 84,1%. Damit beträgt die Fläche links von -1 (1-0,841) und damit 15,9%
[2] Zur Berechnung des z-Wertes muss zuerst der Standardfehler über 3/500,5 = 0,42 berechnet werden. Der z-Wert ergibt sich dann aus: (15-14)/0,42 = 2,38. Wird der Wert des Standardfehlers nicht gerundet, so ergibt sich der exakte z-Wert von 2,357.