Korrelation nach Spearman
Zusammenhangsmaße sind - wie der Name schon sagt - Maße, mit deren Hilfe der Zusammenhang zwischen Merkmalen beschrieben werden kann. In der Praxis häufig anzutreffen sind:
- Kovarianz
- Korrelation (nach Pearson oder Spearman)
Die Korrelation nach Spearman wird verwendet, wenn zumindest ein Merkmal ordinal skaliert ist.
Die Formel zur Berechnung der Korrelation nach Spearman lautet:
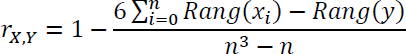
Die Interpretation der Korrelation nach Spearman ist ident mit der Interpretation der Korrelation nach Pearson. Daher sei bezüglich der Interpretation der Korrelation auf die Seite Korrelation verwiesen.
An dieser Stelle wird vielmehr anhand eines Beispiels gezeigt, weshalb die Korrelation nach Pearson nur in Ausnahmefällen mit jener nach Spearman ident ist.
Betrachten Sie dazu die Angaben in den beiden Tabellen 1 und 2. Hervorgehoben ist jene Zelle, in der der Unterschied in den Angaben zu finden ist. Beachten Sie, dass in beiden Fällen die Merkmalsausprägungen von A und B für die Beobachtung 1 am kleinsten sind.
|
|
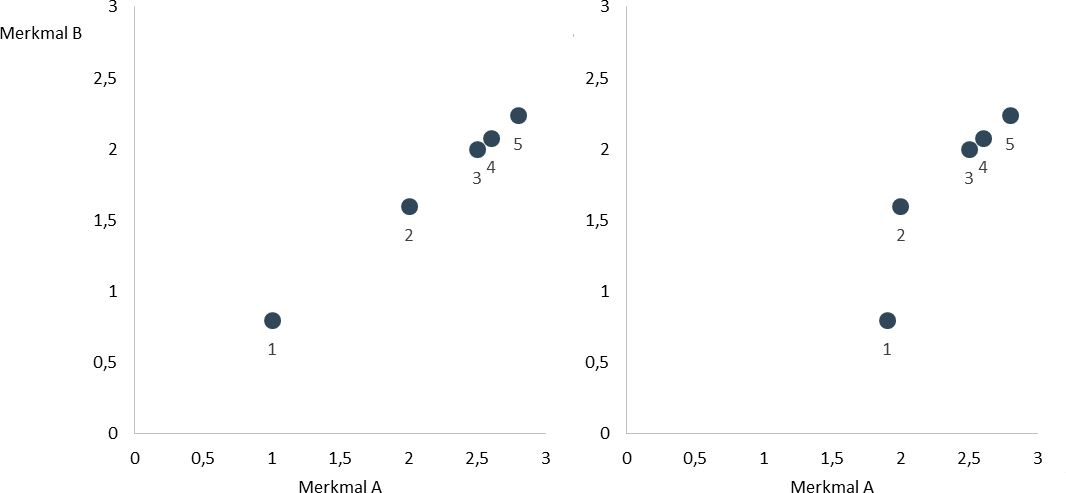
Im ersten Fall beträgt die Korrelation nach Pearson exakt 1. In Fall 2 hingegen "bestraft" Pearson gewissermaßen die horziontale Abweichung der Beobachtung 1 von der gedachten Geraden und weisst dementsprechend eine Korrelation von 0,91 aus.
Da bei der Korrelation nach Spearman ausschließlich die ordinale Information, die in den Daten enthalten ist, verwendet wird, beträgt die Korrelation nach Spearman in beiden Fälle exakt 1. Die nachstehenden Tabellen sollen dies verdeutlichen.
Werden die einzelnen Merkmalsausprägungen in Ränge umgewandelt, so geht die metrische Information verloren. Es geht also die Information verloren, wie groß bspw. der Abstand zwischen den einzelnen Merkmalsausprägungen ist. Dies ist genau so, wie im Skisport. Dort ist jener Skifahrer Sieger, der die kürzeste Fahrzeit hat. Zweitplatzierter ist jener Fahrer mit der zweitlängsten Fahrzeit. Von der Platzierung alleine ist es damit unmöglich auf die Zeiten zu schließen. Umgekehrt ist es egal wie langsam der Zweitplatzierte im Vergleich zum Sieger war, Hauptsache er war scheller als der Drittplatzierte.
|
|
Fassen wir die Diskussion zusammen.
- Die Korrelation nach Spearman ist ein Maß für den linearen Zusammenhang.
- Die Korrelation nach Spearman ist dimensionslos.
- Die Korrelation nach Spearman sagt etwas über die Richtung des Zusammenhangs aus.
- Im Gegensatz zur Kovarianz sagt die Korrelation nach Spearman auch etwas über die Stärke des Zusammenhangs aus.
- Die Korrelation nach Spearman kann nur berechnet werden, wenn beide Merkmale mindestens ordinal skaliert sind.
- Aber ACHTUNG: Interpretieren Sie die Korrelation nach Spearman nie im Sinne eines Steigungskoeffizienten.
Umsetzung in SPSS
- Wählen Sie Analysieren ⟶ Korrelation ⟶ Bivariat...
[1] Beobachtung 1 wurde dazu horizontal auf 3 bzw. vertikal auf 2,5 verschoben.