Statistik

Was, wenn die Varianz unbekannt ist?

---

Ist die Varianz der Grundgesamtheit nicht bekannt, so muss diese geschätzt werden. Dies geschieht, indem zunächst die Varianz der Stichprobe berechnet wird. Die Formel dazu lautet

Beachten Sie: Diese Formel gibt Ihnen die Varianz der Stichprobe. Diese können Sie tatsächlich beobachten.

Man kann nun beweisen, dass die solcherart berechnete Varianz der Stichprobe, die Varianz der Grundgesamtheit systematisch unterschätzt. Man sagt dazu, dass die Varianz der Stichprobe kein erwartungstreuer Schätzer für die Varianz der Grundgesamtheit ist.

Glücklicherweise kann aber ebenso gezeigt werden um wie viel die Varianz der Grundgesamtheit unterschätzt wird, weshalb auch der Fehler korrigiert werden kann. Die Formel, die also die Varianz der Grundgesamtheit auf Basis der Stichprobe schätzt, lautet

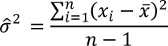
Beachten Sie: Die solcherart geschätzte Varianz können Sie niemals beobachten, da es sich um eine Schätzung für die unbekannte Varianz der Grundgesamtheit handelt.

Haben Sie aber einmal die Varianz der Grundgesamtheit geschätzt, können Sie diese immer anstatt σ² bzw. für σ einsetzen. Wenn Sie dies aber bspw. in der Formel

tun, steht nun nicht mehr nur im Zähler mit x eine Zufallsvariable sondern mit σ nun auch im Nenner. Dies hat zur Folge dass die "z-Werte" nicht mehr normalverteilt sind, sondern t-verteilt, weshalb auch von t-Werten gesprochen wird.

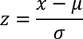
Die entsprechenden Werte sind der Tabelle der t-Verteilung zu entnehmen. Die Unterschiede werden jedoch mit steigender Stichprobengröße kleiner und kleiner. Auf der Seite "Wann die t-Verteilung verwendet wird" ist dies dargestellt.

Zurück zur Übersicht