Wie werden die Wahrscheinlichkeiten bestimmt?
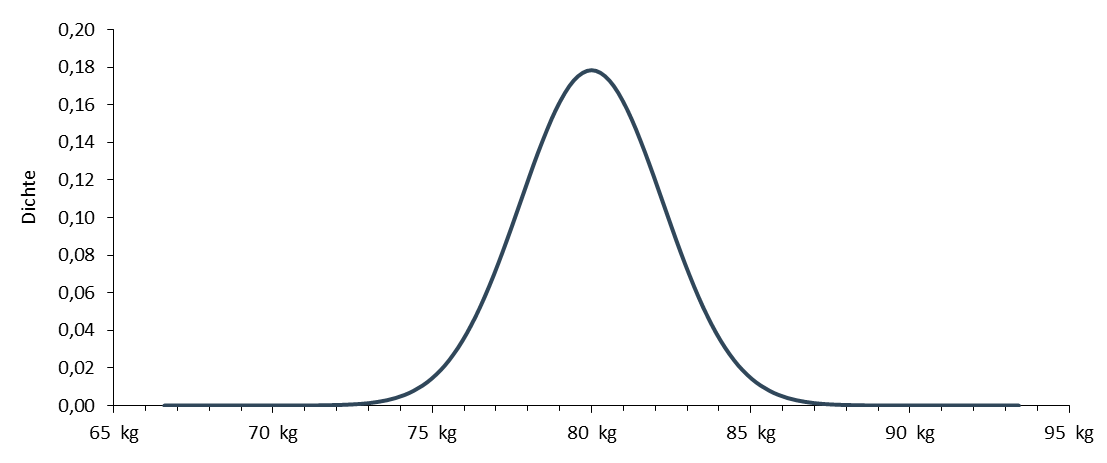
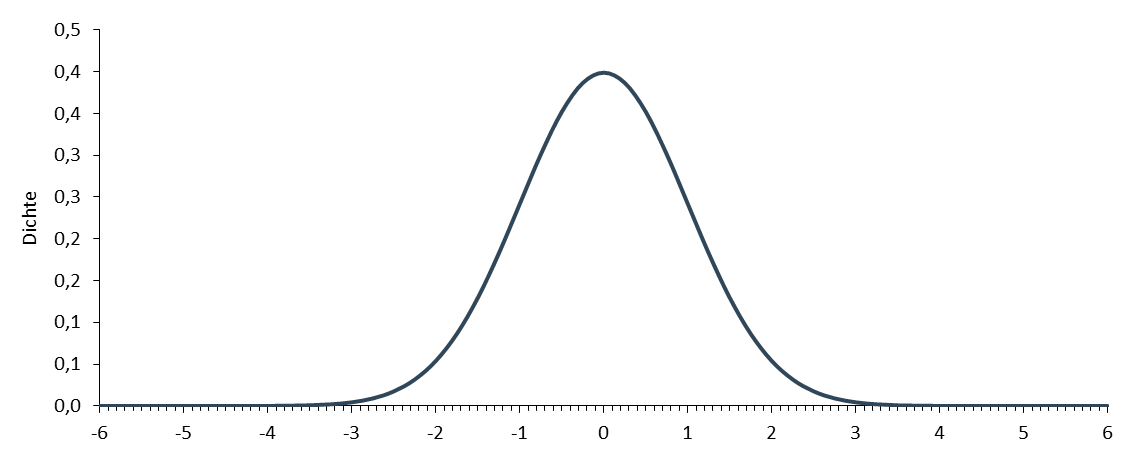
Dieses Beispiel zeigt die Berechnung der Wahrscheinlichkeiten aus dem Beispiel "Was wir wissen, wenn wir alles wissen". Im Beispiel wird das Körpergewicht von Männern betrachtet. Die Ausgangslage ist dabei, dass das mittlere Gewicht (80kg) und die Standardabweichung (3kg) bekannt sind und das Körpergewicht normalverteilt ist. Die folgende Abbildung veranschaulicht dies grafisch.
Diese Verteilung wird allgemein durch die Funktion
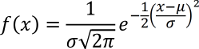
der sog. Dichtefunktion, beschrieben. µ, das Zentrum der Verteilung, ist dabei 80kg und σ, die Standardabweichung, 3kg.
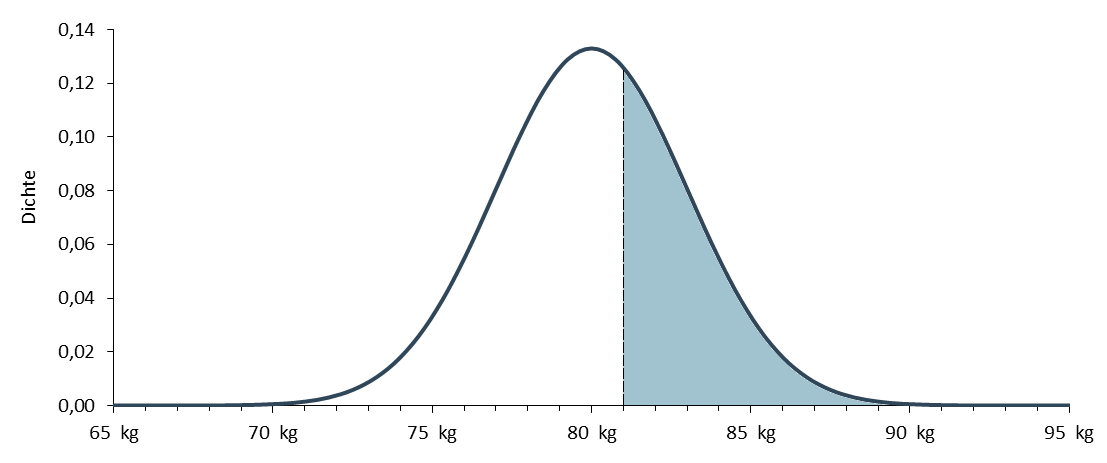
Wie hoch ist der Anteil an Männern mit einem Körpergewicht von mehr als 81kg?
Um diese Frage zu beantworten, könnten Sie zum einen das Integral (von 81kg bis unendlich) über obige Funktion berechnen. Als Ergebnis erhalten Sie die eingefärbte Fläche.
Einfacher ist es aber, wenn die Normalverteilung durch Anwendung der Funktion
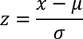
in eine Standardnormalverteilung transformiert wird. Für diese gilt, dass µ immer 0 und σ2 immer 1 ist. Die entsprechende Standardnormalverteilung sieht wie folgt aus.
Ein Körpergewicht von 81kg entspricht einem z-Wert von 0,33, da
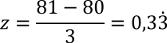
Die gesuchte Fläche in der Standardnormalverteilung ist damit bekannt (eingefärbt).
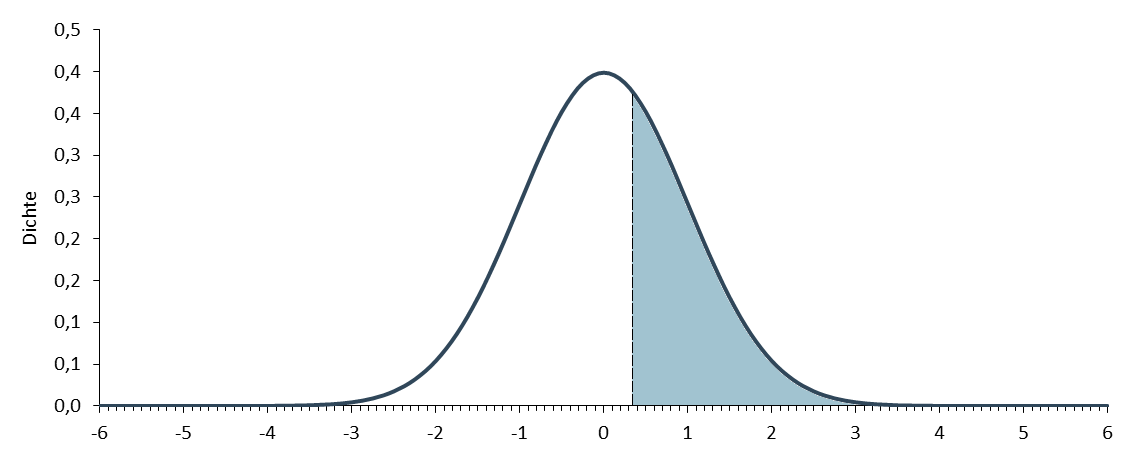
Die Fläche links von 0,33 kann der Tabelle der Standardnormalverteilung entnommen werden und beträgt 0,629. Damit ist die Fläche rechts von 0,33 1 - 0,629 = 0,371 oder 37,1%
Wie hoch ist die Wahrscheinlichkeit bei einer Stichprobe der Größe 40 einen Mittelwert größer als 81kg zu erhalten?
Um diese Frage beantworten zu können, muss die Mittelwertverteilung herangezogen werden. Auch diese wird grundsätzlich durch die obige Dichtefunktion beschrieben. Beachten sie jedoch, dass die Formel nun die Verteilung des Mittelwertes beschreiben soll. Daher muss in die Formel nun die Streuung des Mittelwertes, der Standardfehler, und statt x der Mittelwert von x eingesetzt werden. Man kann sagen, dass wir nun also einen Spezialfall betrachten.
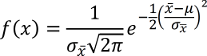
Der Standardfehler errechnet sich dabei wie folgt über die Standardabweichung der Grundgesamtheit
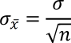
und beträgt 0,474. Die konkrete Verteilung sieht damit wie folgt aus.
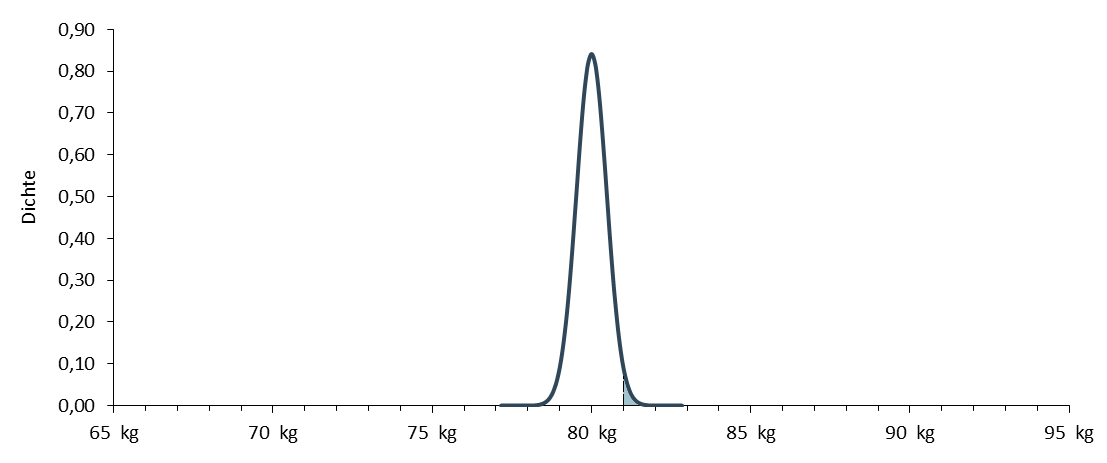
Auch diese Verteilung kann mittels z-Transformation in eine Standardnormalverteilung übergeführt werden und die gesuchte Fläche der Tabelle der Standardnormalverteilung entnommen werden.
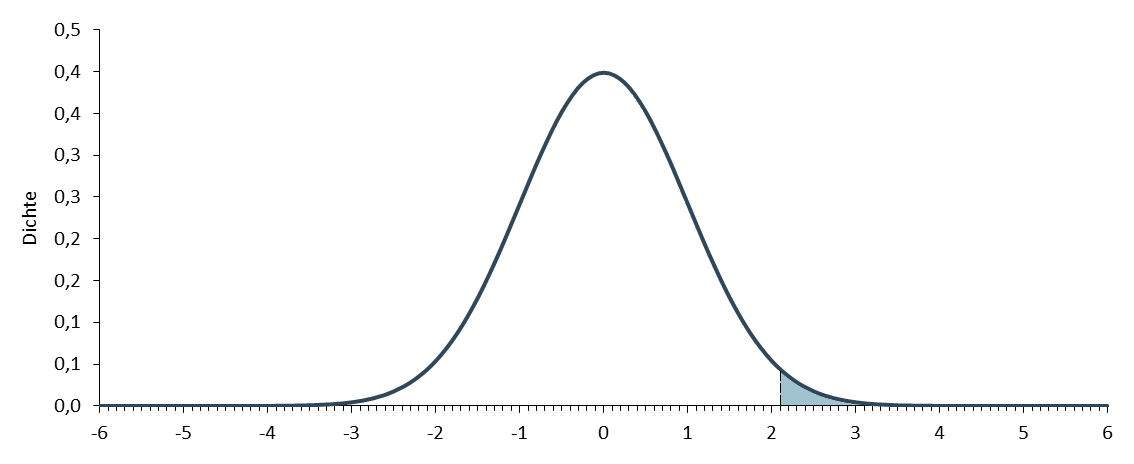
Der gesuchte z-Wert beträgt
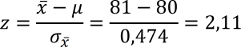
und die entsprechende Fläche rechts davon 1 - 0,983 = 0,017 oder 1,7%. Dies Fläche ist in der Mittelwertverteilung wieder eingefärbt.