Was wir wissen, wenn wir alles wissen
Betrachten wir das Gewicht von Männern. Wenn Sie sich so umsehen, fällt Ihnen natürlich auf, dass nicht alle Männer gleich viel wiegen. In der Statistik sagen wir, dass das Merkmal Gewicht streut. Nehmen wir an, Sie wissen wie hoch diese Streuung ist und Sie wissen auch, wie viel Männer im Durchschnitt wiegen. Außerdem wissen Sie noch, dass das Gewicht normalverteilt ist. Konkret wissen Sie, dass das durchschnittliche Gewicht 80kg und die Streuung, die Standardabweichung, 3kg beträgt.
Wenn Sie das alles wissen, dann können Sie die Verteilung des Gewichts auch grafisch veranschaulichen und erhalten nachfolgendes Bild.
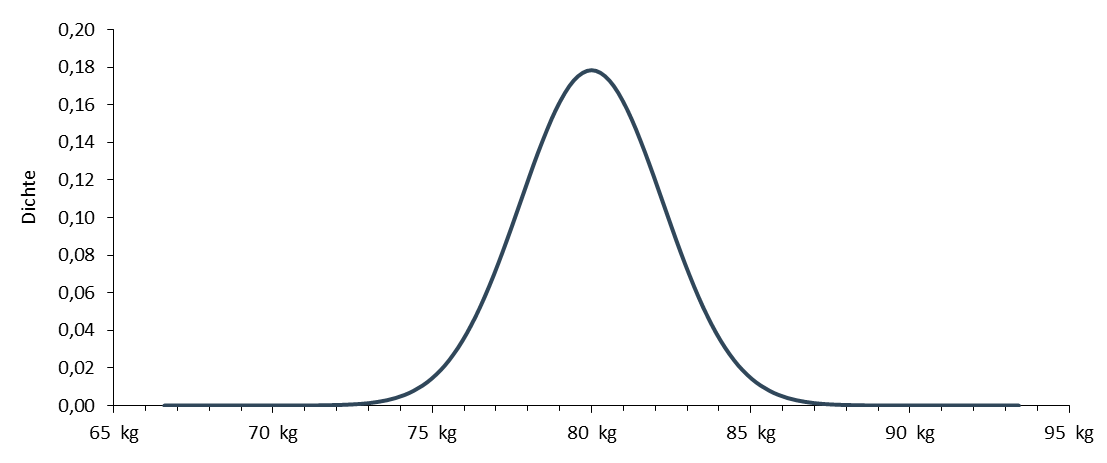
Basierend auf diesem Wissen können Sie drei unterschiedliche Überlegungen anstellen, die letztlich aber alle zusammenhängen. Die Überlegungen sind:
| Wie viel Prozent der Männern wiegen mehr als 81kg? | |
| Wenn Sie zufällig einen (1) Mann auswählen und nach dem Gewicht fragen, wie hoch ist die Wahrscheinlichkeit, dass dieser mehr als 81kg wiegt? | |
| Wenn Sie zufällig 40 Männer auswählen und nach dem Gewicht fragen, wie hoch ist die Wahrscheinlichkeit, dass das durchschnittliche Gewicht dieser 40 Männer höher als 81kg ist? |
Die Antworten auf die Fragen sind ...
Wie viel Prozent der Männern wiegen mehr als 81kg?
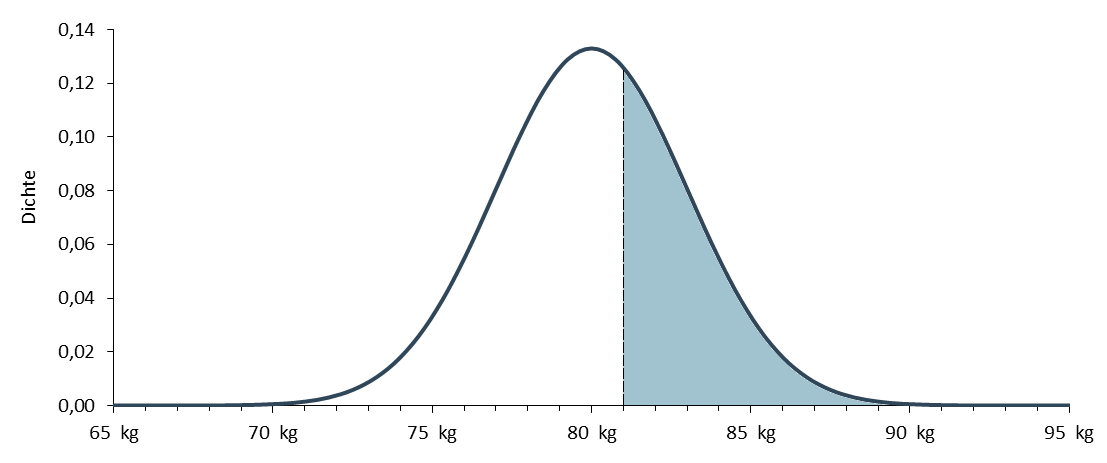
Um die erste Frage beantworten zu können, müssen Sie die eingefärbte Fläche der nachfolgenden Abbildung bestimmen. Diese beträgt 37,1%.
Damit ist der Anteil an Männern mit einem Gewicht von über 81kg 37,1%.
Wenn Sie zufällig einen (1) Mann auswählen und nach dem Gewicht fragen, wie hoch ist die Wahrscheinlichkeit,
dass dieser mehr als 81kg wiegt?
Um diese Frage beantworten zu können, müssen Sie wissen wie viel Prozent der Männer ein Gewicht von über 81kg hat - und das tun Sie. Es sind 37,1%.
Damit beträgt die Wahrscheinlichkeit, dass ein zufällig befragter Mann mehr als 81kg wiegt, 37,1%. Die Antwort ist also dieselbe.
Aber wo liegt dann der Unterschied zur ersten Frage, und wo der Zusammenhang?
Der Unterschied ist, dass die erste Frage darauf abzielt, wie viel Prozent aller Männer ein Gewicht von über 81kg haben. Frage zwei zielt auf die Wahrscheinlichkeit ab, dass das Gewicht eines zufällig befragten Mannes größer als 81kg ist. Der Zusammenhang ist, dass diese Wahrscheinlichkeit 1:1 mit dem Anteil an Männern mit mehr als 81kg Körpergewicht zusammenhängt.
Wenn Sie zufällig 40 Männer auswählen und nach dem Gewicht fragen, wie hoch ist dann die Wahrscheinlichkeit,
dass das durchschnittliche Gewicht dieser 40 Männer höher als 81kg ist?
Um diese Frage beantworten zu können, müssen Sie sich eines vor Augen halten. Sie könnten ja eigentlich sehr, sehr oft jeweils 40 Männer nach ihrem Gewicht befragen
und jeweils das durchschnittliche Gewicht berechnen. Sie würden damit sehr viele unterschiedliche Mittelwerte erhalten. Das heißt aber, dass auch die Mittelwerte Ihrer
Stichproben streuen - und zwar so, wie in der nächsten Abbildung dargestellt.
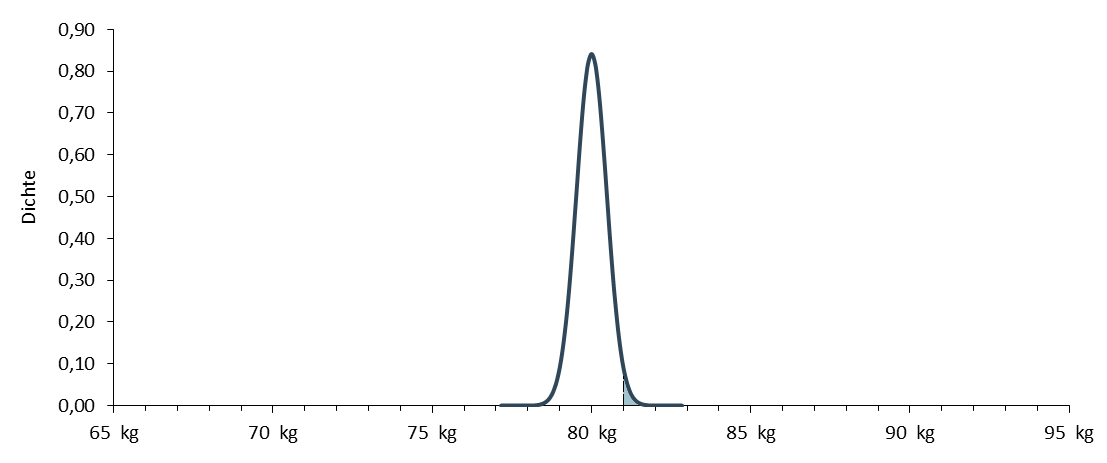
Beachten Sie, wie schmal diese Verteilung im Vergleich zur oberen ist. Dies bringt zum Ausdruck, dass die Mittelwerte viel weniger streuen als das Gewicht selbst. Der Grund dafür ist, dass rund 90% der Männer ein Gewicht zwischen 75 und 85kg haben und es ausgesprochen unwahrscheinlich ist, dass eine zufällig gezogene Stichprobe nur Männer enthält, die bspw. überduchschnittlich schwer sind. Die Wahrscheinlichkeit, einen Mittelwert über 81kg zu erhalten beträgt übrigens nur noch 1,7%.
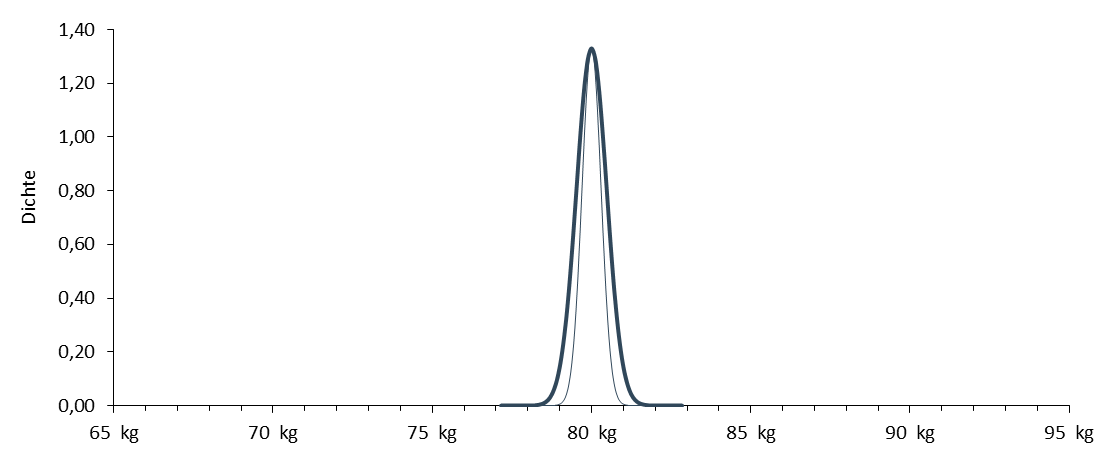
Beachten Sie dabei, dass diese Wahrscheinlichkeit von der Breite der Mittelwertverteilung abhängt und die Breite wiederum von der Stichprobengröße (nicht aber die Mitte der Verteilung, die ist immer 80kg). Die nächste Abbildung zeigt dünn eingezeichnet die Mittelwertverteilung für eine Stichprobengröße von 100. Wie Sie sehen, wird die Verteilung schmaler, wenn die Stichprobengröße steigt. Damit sinkt aber auch die Wahrscheinlichkeit, dass ein Stichprobenmittelwert größer 81kg gezogen wird.
In der schließenden Statistik werden meist Fragen der letzten Art beantwortet.
Wie die in diesem Text genannten Wahrscheinlichkeiten bestimmt werden, erfahren Sie auf der Seite "Warum die Standardnormalverteilung praktisch ist". Die Lösung zu diesem Beispiel finden Sie auf der Seite "Wie werden die Wahrscheinlichkeiten bestimmt?".
Was sich ändert, wenn die Varianz unbekannt ist, lesen Sie auf der Seite "Wann die t-Verteilung verwendet wird" bzw. "Was, wenn die Varianz unbekannt ist?".