Arithmetisches Mittel, Modus, Median & Co.
Lagemaße, auch Maße der zentralen Tendenz genannt, sind Kennwerte, die gewissermaßen für eine typische bzw. repräsentative Beobachtung stehen. In der Praxis am häufigsten anzutreffen sind:
- arithmetische Mittel
- Median
- Modus (auch Modalwert genannt)
- geometrische Mittel
Die Beispiele zum arithmetischen Mittel, Median bzw. Modus basieren dabei auf den in der Tabelle wiedergegebenen Daten.
| Person 1 | Person 2 | Person 3 | Person 4 | Person 5 | Person 6 | Person 7 | Person 8 | Person 9 |
|---|---|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 9 | 7 | 5 | 4 | 5 | 1 |
Arithmetisches Mittel
Das arithmetische Mittel wird berechnet, indem die Summe aller Werte durch die Anzahl aller Werte dividiert wird.
Das arithmetische Mittel beträgt im vorliegenden Beispiel 5,44.
Median
Der Median wird so gefunden, indem jener Wert gesucht wird, der die geordneten Werte derart aufteilt, dass darunter und darüber gleich viele Fälle liegen. Er beträgt im vorliegenden Beispiel 5.
| 1 | 4 | 5 | 5 | 5 | 6 | 7 | 7 | 9 |
Bei einer geraden Anzahl an Messwerten entspricht der Median dem arithmetischen Mittel der beiden "mittleren" Werte. Hätten wir also bspw. lediglich die Werte der Personen 1 bis 4, so wäre der Median 6,5.
Modus
Der Modus ist jener Wert, der am häufigsten vorkommt. Er beträgt im vorliegenden Beispiel 5.
| 1 | 4 | 5 | 5 | 5 | 6 | 7 | 7 | 9 |
Gibt es mehrere Werte, die gleichhäufig vorkommen, so spricht man von einer multimodalen Verteilung.
Geometrische Mittel
Das folgende Beispiel soll zeigen, weshalb Sie bei Wachstumsraten nicht das arithmetische Mittel, sondern das geometrische Mittel berechnen sollten.
Stellen Sie sich vor, Sie können € 100 für 2 Jahre zu einem Zinssatz von 10% (Wachstumsrate des Kapitals) anlegen. Wie das Beispiel zeigt, hätten Sie nach 2 Jahren einen Betrag von € 121 angespart.
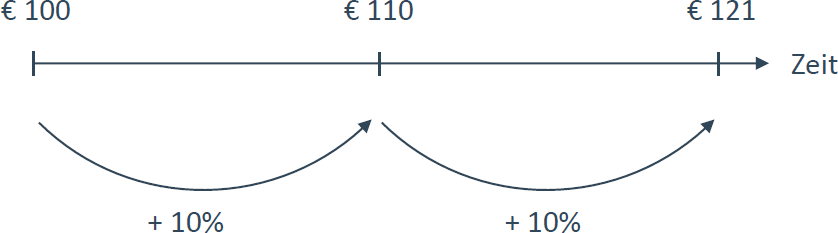
Wenn Sie alternativ die € 100 für 2 Jahre derart veranlagen könnten, dass Sie im 1 Jahr keine Zinsen und im 2 Jahr einen Zinssatz von 20% erhalten, dann hätten Sie nach 2 Jahren lediglich € 120 angespart - also um € 1 weniger als im ersten Fall und das, obwohl die mittlere Verzinsung (=arithmetisches Mittel) in beiden Fällen gleich ist. Für den Unterschied ist der Zinseszinseffekt verantwortlich.
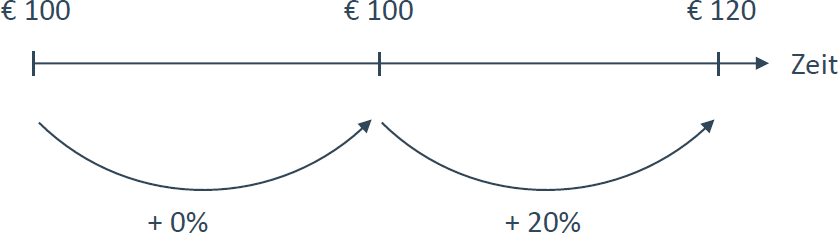
Das geometrische Mittel berechnet sich nun wie folgt:
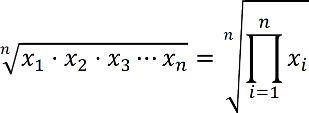
Im zweiten Fall beträgt das geometrische Mittel demnach 9,54%
Beachten Sie, dass im Falle subjektiver Empfindungsstärken häufig das geometrische Mittel besser den Durchschnitt beschreibt als das arithmetische Mittel, weshalb auch in diesen Fällen dem Ersteren der Vorzug gegeben werden sollte.
Umsetzung in SPSS
- Wählen Sie Analysieren ⟶ Deskriptive Statistiken ⟶ Häufigkeiten...
- Unter Statistik finden Sie die Lagemaße.