Korrelation nach Pearson
Zusammenhangsmaße sind - wie der Name schon sagt - Maße, mit deren Hilfe der Zusammenhang zwischen Merkmalen beschrieben werden kann. In der Praxis häufig anzutreffen sind:
- Kovarianz
- Korrelation (nach Pearson oder Spearman)
Die Korrelation nach Pearson wird bei metrisch skalierten Merkmalen verwendet und basiert auf der Idee der Kovarianz.
Die Formel zur Berechnung der Korrelation nach Pearson lautet:
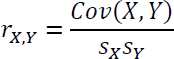
Die Korrelation wird durch die Division normiert, weshalb sie ausschließlich Werte von -1 bis +1 annehmen kann. Dies ist auch der Grund, weshalb die Korrelation neben der Richtung auch etwas über die Stärke des Zusammenhangs aussagt.
Die Interpretation der Korrelation nach Pearson sei anhand konkreter Beispiele veranschaulicht. Um die Unterschiede zwischen den Zusammenhangsmaßen besser herausarbeiten zu können, sind die Beispiele immer die gleichen. Die Daten sind auf der Seite Kovarianz zu finden.
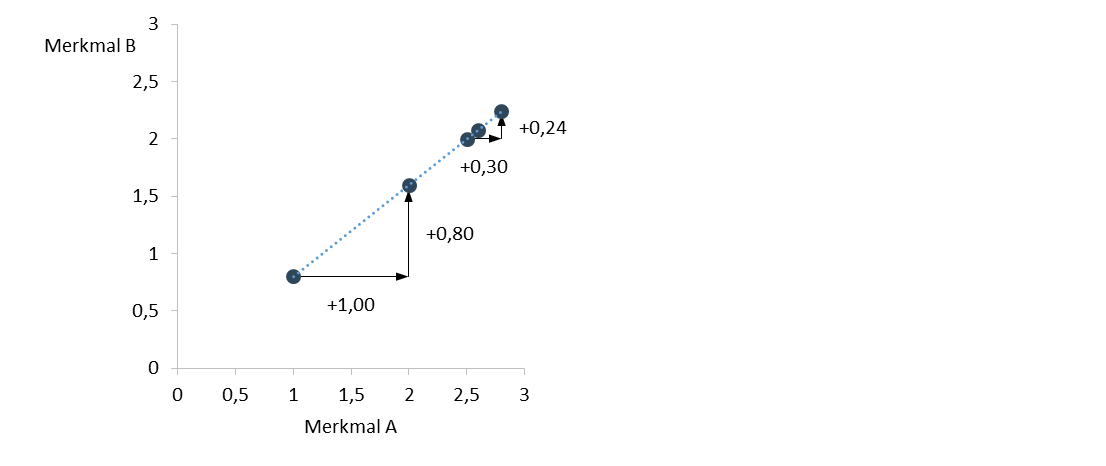
Nachfolgende Abbildung zeigt grafisch den Zusammenhang zwischen zwei Merkmalen A und B. Wie Sie erkennen können, ist der Zusammenhang perfekt, da alle Punkte auf einer gedachten Geraden liegen. Die Steigung dieser Geraden beträgt 0,8 und besagt, dass ein Anstieg des Merkmals A um 1 Einheit zu einem Anstieg bei Merkmal B um 0,8 Einheiten führt.
Die Korrelation beträgt im Beispiel jedoch 1, womit bereits der wichtigste Punkt veranschaulicht ist:
- Interpretieren Sie die Korrelation niemals als Steigung.
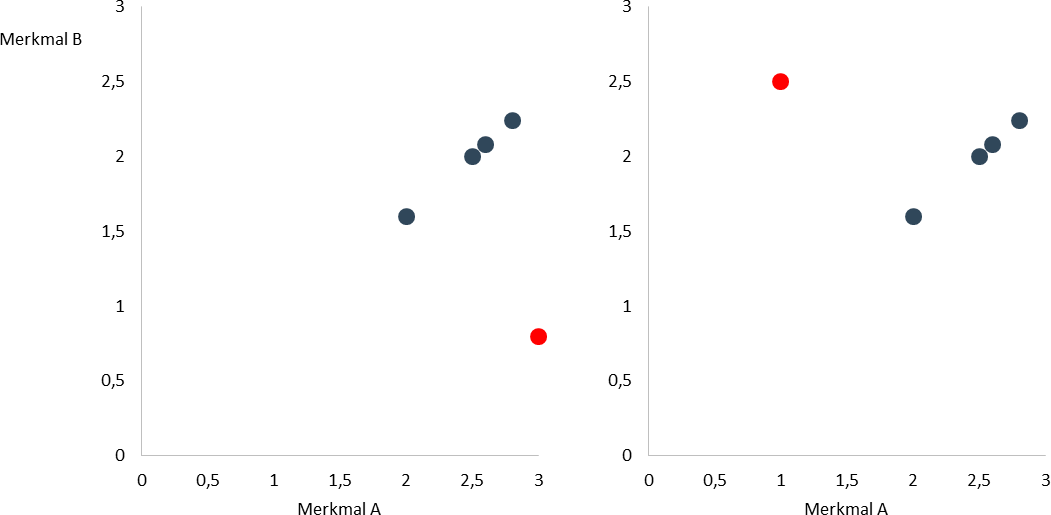
Die nächsten zwei Abbildungen sollen veranschaulichen, dass sich der visuelle Eindruck vom Zusammenhang verändert, wenn die erste Beobachtung nach rechts oder oben verschoben wird (Beachten Sie: Dies ist nicht der Fall, wenn die Beobachtung nach links oder unten verschoben wird.). Das negative Vorzeichen der Korrelation spieglt das wider. Im linken Beispiel beträgt die Korrelation -0,25 und im rechten -0,35. [1]
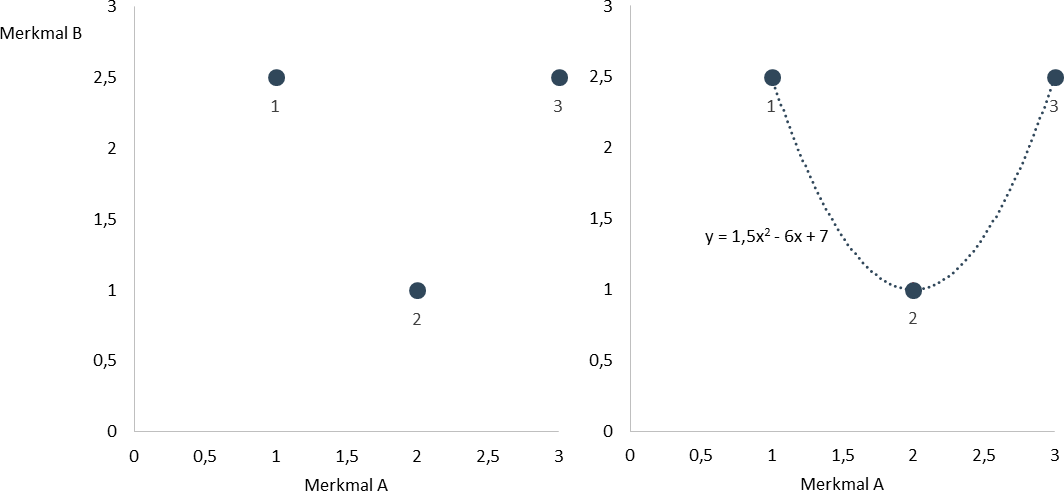
Da die Korrelation nach Pearson auf der Kovarianz beruht, gilt auch für die Korrelation, dass sie bei nichtlinearen Zusammenhängen nicht verwendet werden sollte.
In anderen Worten bedeutet dies, dass im untenstehenden Beispiel nicht nur die Kovarianz sondern auch die Korrelation Null ist.
Die zwei Vorteile der Korrelation gegenüber der Kovarianz veranschaulichen die nächsten beiden Beispiele.
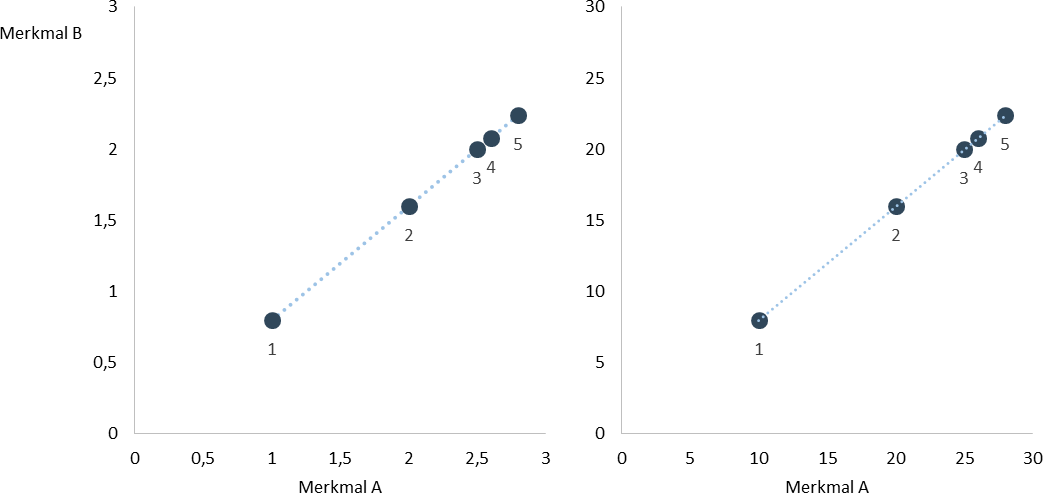
Der erste Vorteil gegenüber der Kovarianz ist, dass ihr Wert unabhängig von der Einheit ist, in der die Variablen gemessen werden. D.h., es macht keinen Unterschied, ob bspw. die Einkommen und Ausgaben von Personen in Euro oder in Eurocent gemessen werden. Sowohl im Beispiel links als auch im Beispiel rechts beträgt die Korrelation 1.
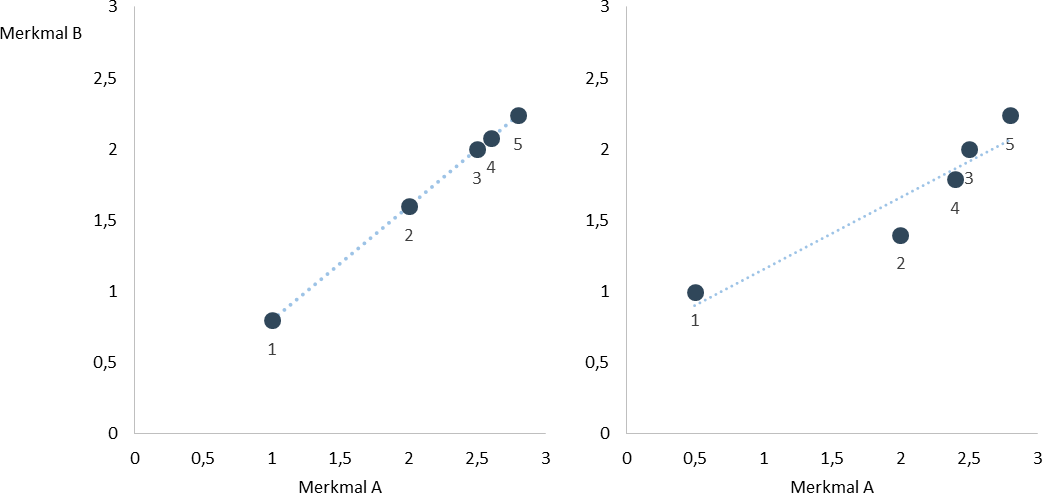
Der zweite Vorteil gegenüber der Kovarianz ist, dass ihr Wert etwas über die Stärke des Zusammenhangs aussagt. Im Beispiel links beträgt die Korrelation wieder 1, im Beispiel rechts beträgt die Korrelation 0,94.
Fassen wir die Diskussion zusammen.
- Die Korrelation nach Pearson ist ein Maß für den linearen Zusammenhang.
- Die Korrelation nach Pearson ist dimensionslos.
- Die Korrelation nach Pearson sagt etwas über die Richtung des Zusammenhangs aus.
- Im Gegensatz zur Kovarianz sagt die Korrelation nach Pearson auch etwas über die Stärke des Zusammenhangs aus.
- Die Korrelation nach Pearson kann nur berechnet werden, wenn beide Merkmale metrisch skaliert sind.
- Aber ACHTUNG: Interpretieren Sie die Korrelation nach Pearson nie im Sinne eines Steigungskoeffizienten.
Umsetzung in SPSS
- Wählen Sie Analysieren ⟶ Korrelation ⟶ Bivariat...
[1] Beobachtung 1 wurde dazu horizontal auf 3 bzw. vertikal auf 2,5 verschoben.