Konfidenzintervalle - Das Vertrauen in den Zufall (Teil 2)
Stellen Sie sich vor, Sie kennen basierend auf einer Stichprobe das Körpergewicht von 30 Männern. Der Stichprobenmittelwert beträgt 70kg. Die Streuung 14kg.

Aus der Diskussion Was wir wissen, wenn wir alles wissen wissen Sie, dass dieser Mittelwert aus einer Grundgesamtheit stammt, deren Zentrum das "wahre" durchschnittliche Gewicht von Männern ist. Aber in diesem Beispiel kennen Sie dieses Zentrum nicht - und deshalb drehen wir die Frage ganz einfach um, indem wir uns nun fragen:
| Wie weit dürfte das Zentrum µ der wahren Verteilung maximal von 70kg entfernt sein, sodass bei einem Hypothesentest die Annahme, dass µ der wahre Wert der Verteilung ist, gerade nicht verworfen wird? |
Ein Beispiel soll die Fragestellung wieder illustrieren.
Stellen Sie sich vor, dass Sie noch bevor Sie die Stichprobe ziehen, glauben, dass Männer im Schnitt 60kg wiegen. Würden Sie an dieser Annahme festhalten, wenn das Gewicht in Ihrer zufällig gezogenen Stichporbe im Schnitt 70kg beträgt? Naja, um das zu entscheiden, können Sie sich einfach ausrechnen, wie hoch die Wahrscheinlichkeit ist, einen Stichprobenmittelwert von 70kg zu erhalten, wenn das wahre durchschnittliche Gewicht tatsächlich 60kg beträgt.
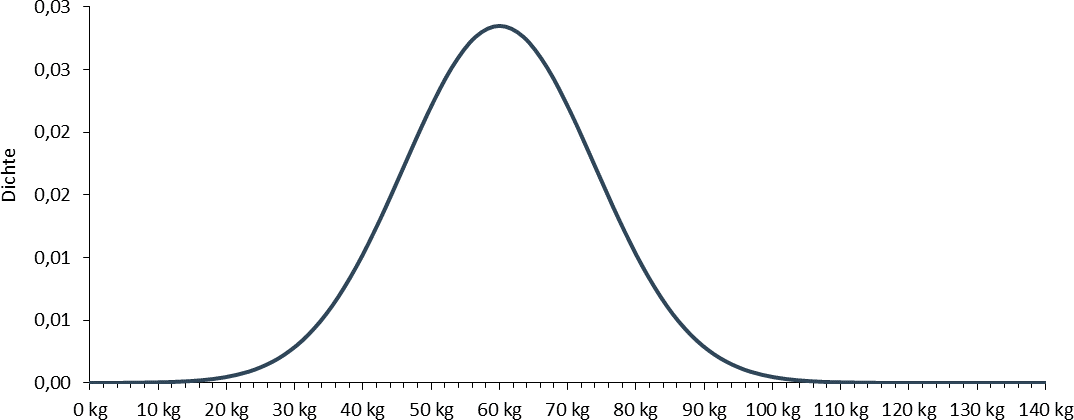
Um diese Frage beantworten zu können, müssen Sie die Mittelwertverteilung kennen - und das tun Sie, weil Sie "kennen" das Zentrum der wahren Verteilung und können über die Varianz der Stichprobe die Varianz der Grundgesamtheit - wie in "Was, wenn die Varianz unbekannt ist?" gezeigt - schätzen. Die Verteilung des Mittelwertes sieht wie folgt aus.
Die Fläche, die rechts von 70kg unter der Verteilung liegt, ist zusätzlich herausgezoomt, weil wir sonst nicht viel erkennen können. Diese Fläche beträgt 0,008% (z-Wert 3,78). Die Wahrscheinlichkeit ist also extrem gering, dass wenn das wahre durchschnittliche Gewicht 60kg beträgt, Sie diese konkrete Stichprobe erhalten. Daher würden Sie an Ihrer Annahme nicht mehr festhalten - die Abweichung ist einfach zu groß. Aber welche Abweichung wäre dann gerade noch klein genug?
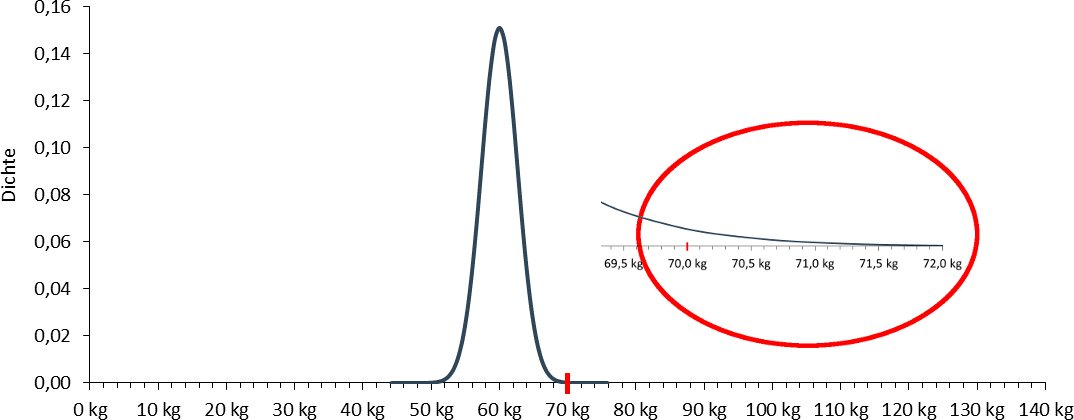
Nehmen wir dazu an, Sie würden die Annahme immer dann verwerfen, wenn Ihr Stichprobenergebnis von 70kg - also die Beobachtung - eine Wahrscheinlichkeit von kleiner 2,5% hat. Das Procedere lautet:
Auf Basis der Stichprobenvarianz wird die Populationsvarianz über
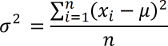
geschätzt.
Aufbauend darauf schätzen Sie über
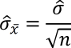
den Standardfehler, also die Streuung der Mittelwerte.
Durch Umformung der Formel
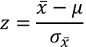
nach µ erhalten Sie für einen z-Wert von 1,96 ein µ von 64,82kg. Die Abbildung zeigt die entsprechende Verteilung.
D.h., beträgt das wahre durchschnittliche Gewicht in der Grundgesamtheit 64,82kg, wird eine Stichprobe der Größe 30, die ein durchschnittliches Gewicht von 70kg (oder höher) aufweist, mit einer Wahrscheinlichkeit von 2,5% gezogen.
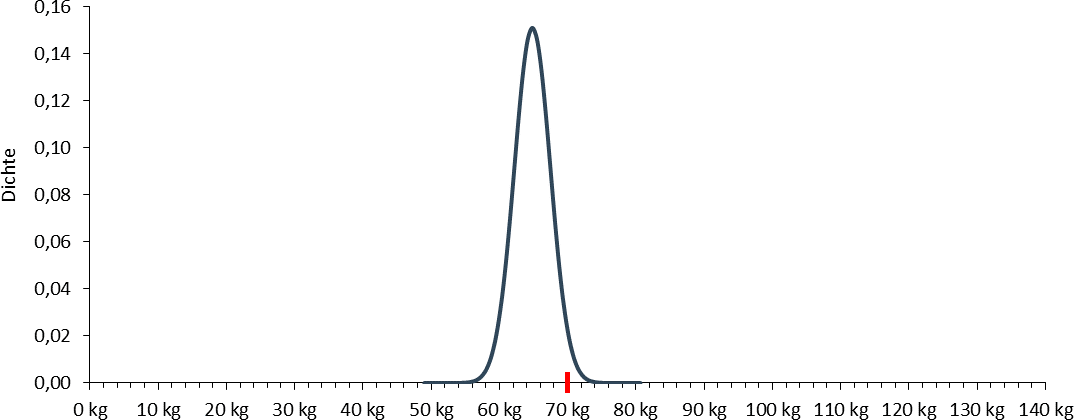
Jede Verteilung, die nach unten weniger weit abweicht, bedeutet gleichzeitig, dass die Wahrscheinlichkeit, in einer Stichprobe ein Gewicht von 70kg zu erhalten, höher ist.
Jetzt muss nur noch die analoge Überlegung in die andere Richtung angestellt werden, also 70 + 5,18 gerechnet werden.
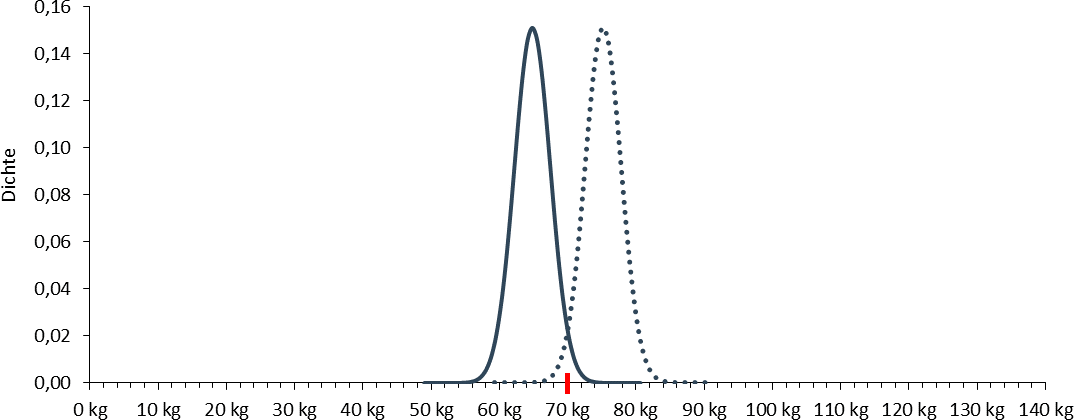
Und nun vergleichen Sie das Ergebnis mit der Diskussion auf der Seite "Konfidenzintervalle - Das Vertrauen in den Zufall (Teil 1)".
Dort wird beschrieben, dass das Konfidenzintervall nach der Formel
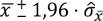
berechnet wird. Das Ergebnis ist ein Konfidenzintervall, das von 64,82kg bis 75,18kg geht.