Konfidenzintervalle - Das Vertrauen in den Zufall (Teil 1)
Starten wir gleich mit der Definition des Konfidenzintervalls:
| "Das Konfidenzintervall gibt jenen Bereich eines Merkmals an, in dem sich (z.B.) 95% aller möglichen Populationsparameter befinden, die den empirisch ermittelten Stichprobenkennwert erzeugt haben können." |
Schön, aber was soll das heißen? Starten wir dazu ganz von vorne ...
Stellen Sie sich vor, Sie kennen eine Grundgesamtheit, die aus 400.000 Beobachtungen besteht. Die genaue Verteilung des Merkmals entnehmen Sie der Abbildung. Mittelwert und Streuung stehen daneben. Den EXCEL-Datensatz dazu finden Sie hier.
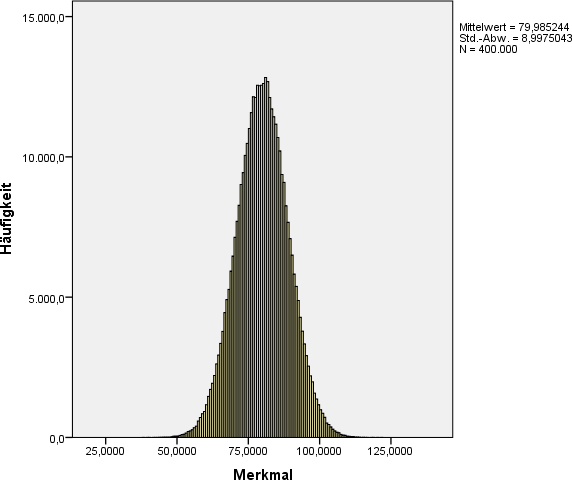
Basierend auf diesen Ergebnissen beträgt der theoretische Standardfehler, also die Streuung der Mittelwerte, von Stichproben der Größe 40
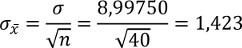
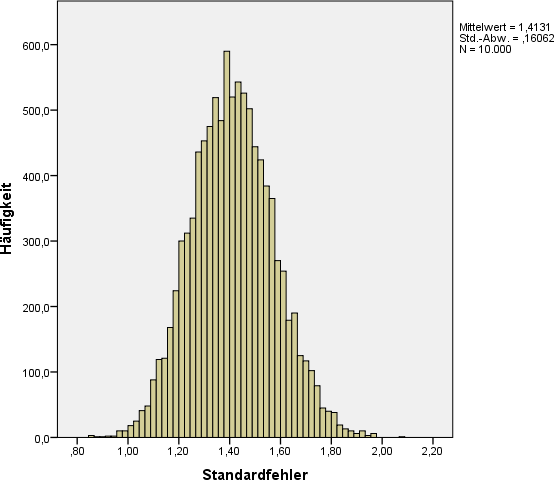
Werden nun aus dieser Grundgesamtheit zufällig 10.000 Stichproben der Größe 40 gezogen, erhält man 10.000 verschiedene Mittelwerte. Die Verteilung dieser 10.000 Mittelwerte sieht dabei wie folgt aus.
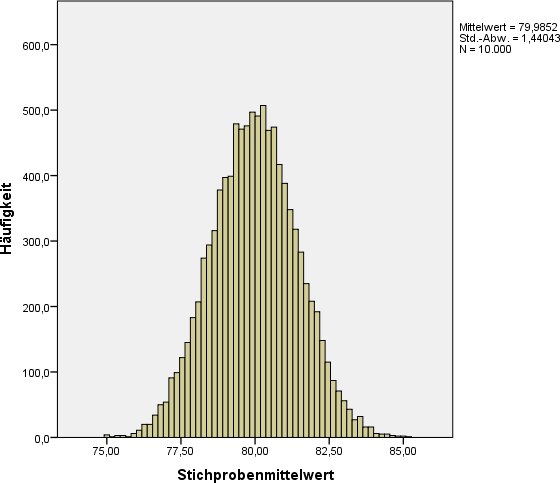
Beachten Sie dabei folgende Punkte
| 1. Die mittlere Streuung stimmt nicht mit der von uns berechneten überein. | |
| 2. Die Mittelwerte der beiden Verteilungen stimmen praktisch überein. | |
| 3. Die Verteilung des Mittelwertes ist schmaler als die Verteilung des Merkmals selbst. |
Punkt 1 ist aber kein "Fehler". Wie auf der Seite "Was, wenn die Varianz unbekannt ist?" besprochen, ist die Stichprobenvarianz kein erwartungstreuer Schätzer für die Varianz der Grundgesamtheit. Wird die Varianz der Grundgesamtheit aus einer Stichprobe geschätzt, muss nämlich folgende Formel verwendet werden.
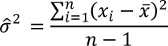
Werden 10.000 mal die 40 Stichprobendaten in diese Formel eingesetzt und dann gemäß
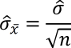
Der mittlere Standardfehler weicht nun nur noch um 0,7% vom theoretisch korrekten ab.
Nun stellen Sie sich Folgendes vor: Sie verwenden die 10.000 Stichprobenmittelwerte und die 10.000 Standardfehler und setzen diese in folgende Formel ein.
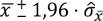
In Worten: Für jede Stichprobe ziehen Sie einmal 1,96 Standardfehler vom Stichprobenmittelwert ab und einmal 1,96 Standardfehler dazu. Sie erhalten so für jede Stichprobe einen "unteren" und einen "oberen" Wert und somit 10.000 Intervalle. Alle Intervalle sind unterschiedlich breit und haben eine andere Mitte. Exemparisch sei dies für die ersten 20 Stichproben illustriert.
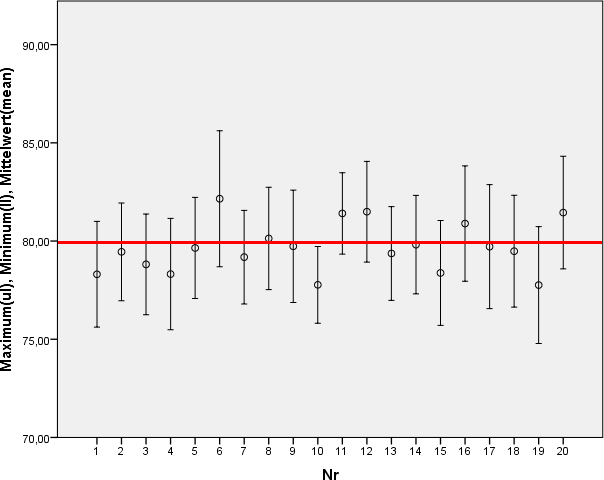
Würden wir dies für alle 10.000 Stichproben veranschaulichen, würden wir Folgendes sehen: Die rote Linie geht durch etwas mehr als 94% aller Intervalle durch. Die rote Linie läuft damit lediglich an 6% aller Intervalle vorbei (bspw. durch Intervall Nr. 10). Die Rote Linie steht aber für den Mittelwert der Grundgesamtheit - und das ist die Idee des Konfidenzintervalls . In der Statistik hört sich das dann so an:
| Noch bevor Sie die (1) Stichprobe ziehen, können Sie sagen, dass, wenn Sie ein Intervall nach obiger Formel berechnen, dass dieses Intervall mit einer Wahrscheinlichkeit von 95% den wahren Mittelwert der Grundgesamtheit enthält. |
Wenn Sie den Wert 1,96 ändern - dies ist der z-Wert, der rechts und links von der Normalverteilung 2,5% abschneidet - ändern Sie auch die Wahrscheinlichkeit, mit der das Intervall den wahren Wert enthält.
Aber Achtung: In der Praxis kennen Sie den wahren Wert der Grundgesamtheit nicht. Daher gilt:
| Nachdem Sie das Intervall berechnet haben, können Sie das nicht mehr sagen. Nachdem das Intervall berechnet wurde, liegt der wahre Wert entweder im Intervall oder nicht (vgl. Nr. 10) - Sie werden das aber nie wissen. |
D.h., es muss schon viel Pech im Spiel sein, dass Sie durch Zufall ein Intervall erhalten, das den wahren Wert nicht enthält. Oder anders formuliert: Sie können relativ zuversichtlich sein, dass das solcherart berechnete Intervall, den wahren (aber unbekannten) Wert der Grundgesamtheit enthält.
Damit bleiben aber zwei Fragen offen:
Frage Warum enthalten im Beispiel 96% aller Intervalle den wahren Mittelwert und nicht 95%?
Antwort Weil unsere Stichprobe und die Grundgesamtheit schlicht zu kein sind. Theoretisch müssten beide unendlich groß sein.
Frage Geht die eingangs eingeführte Definition nicht genau anders rum?
Diese besagt doch, dass 95% aller "in Frage kommender" Populationsparameter im Konfidenzintervall enthalten sind.
Das Beispiel argumentiert aber genau umgekehrt nämlich, dass von allen denkbaren Konfidenzintervallen 95% genau den einen (1) richtigen Populationsparameter enthalten.
Antwort Stimmt. Aber das ist nur eine andere Betrachtung. Warum, das zeigt "Konfidenzintervalle - Das Vertrauen in den Zufall (Teil 2)".