Zweiseitiger Hypothesentest
Stellen Sie sich vor, Sie glauben auf Grund von Erzählungen, dass ein Medizinstudium im Durchschnitt 15 Semester dauert. Das wäre Ihre Nullhypothese. Da Sie jedoch nicht wissen, ob Sie dieser Information trauen können, ziehen Sie eine Stichprobe und beobachten in der Stichprobe eine durchschnittliche Studiendauer von 22 Semester. Dass der beobachtete Mittelwert vom erwarteten abweicht, überrascht Sie natürlich wenig. Die Frage die sich aber stellt ist, ob der Mittelwert "zu weit" abweicht, als dass Sie weiterhin der Information Glauben schenken wollen.
Um diese Frage letztendlich entscheiden zu können, legen Sie, noch bevor Sie die Stichprobe ziehen, die Grenzen fest, ab der Sie gewillt sind die Annahme zu verwerfen. Konkret entschließen Sie sich die Annahme immer dann zu verwerfen, wenn Sie in der Stichprobe einen Mittelwert erhalten, dessen Auftreten unter der Annahme einer durchschnittlichen Studiendauer von 15 Semestern eine Wahrscheinlichkeit von kleiner (gleich) 5% hat. Kurz: Sie entscheiden sich, Ihre Hypothese auf dem 5%-Niveau zu testen.
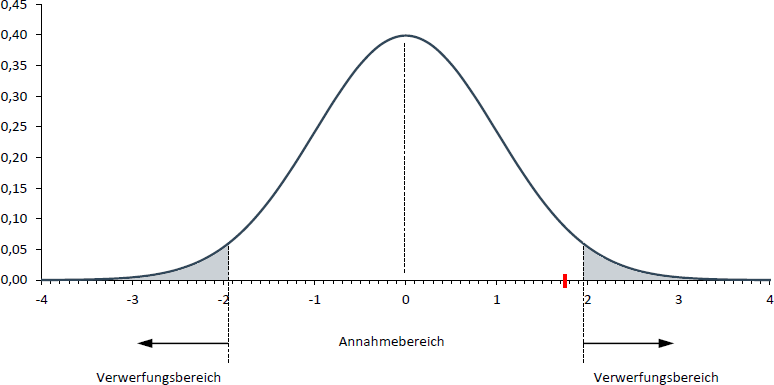
Der Standardnormalverteilungs-Tabelle entnehmen Sie die entsprechenden - sog. kritischen - z-Werte, die links bzw. rechts 2,5% der Standardnormalverteilung abschneiden. Diese betragen plus minus 1,96.
Wenn Sie nun den beobachten Mittelwert z-transformieren (Annahme: der Standardfehler beträgt 4), so erhalten Sie einen empirischen z-Wert von 1,75 (rote Markierung in der folgenden Abbildung). Da dieser Wert zwischen minus 1,96 und plus 1,96 liegt, verwerfen Sie die Annahme nicht. Anders dargestellt: Wenn der empirische z-Wert in den Annahmebereich fällt, verwerfen Sie die Hypothese nicht.
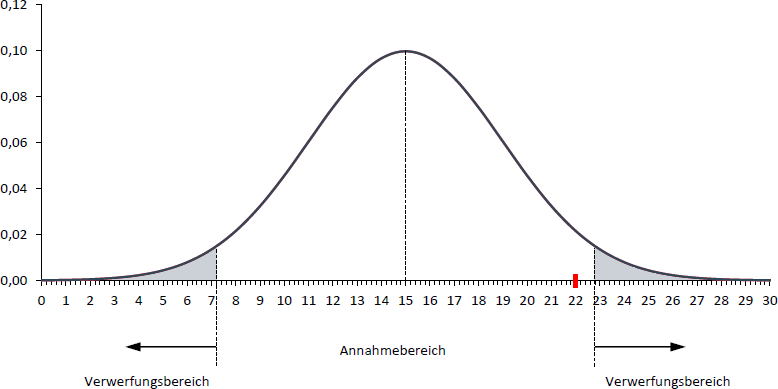
Alternativ können die kritischen z-Werte verwendet werden, um auf die Grenzen ausgedrückt in Semestern "zurückzurechnen" und erhalten so die Grenzen 7,2 bzw. 22,8 Semester. Natürlich fällt der empirisch ermittelte Mittelwert wieder in den Annahmebereich, weshalb die Nullhypothese wieder nicht verworfen wird.
Vergleichen Sie dieses Ergebnis mit jenem des einseitigen Hypothesentests. Abhängig davon, ob die Hypothese einseitig oder zweiseitig getestet wird, wird die Hypothese auf demselben Signifikanzniveau einmal verworfen und einmal akzeptiert.
Eine kleine Anmerkung am Rande: Beachten Sie bitte, dass die beiden Verteilungen lediglich auf Grund des angepassten Maßstabes ähnlich aussehen. Tatsächlich ist die Standardnormalverteilung (obere Verteilung) deutlich schmaler und damit höher als die untere.
Vergleich mit dem einseitigen Hypothesentest.