Die Idee hinter Hypothesentests
Unverbundene Stichproben
Das folgende Beispiel soll ein intuitives Verständnis für die Idee hinter Hypothesentests aufbauen. Ein Verständnis dafür ist deshalb von zentraler Bedeutung, da Sie nur so einschätzen können, was Ihr (inferenzstatistisches) Testergebnis aussagt - und was eben nicht.
Ein Gedankenexperiment
Stellen Sie sich vor, Sie haben eine Münze vor sich liegen und Sie wissen, dass diese Münze mit einer Wahrscheinlichkeit von exakt 50% auf Kopf bzw. Zahl fällt.
Nun werfen Sie die Münze 30-mal, mit dem Ergebnis, dass die Münze 8-mal auf Kopf und 22-mal auf Zahl gefallen ist. Was würden Sie sich in so einem Fall denken?
Wahrscheinlich würden Sie sich so etwas in der Art denken wie: "Was für ein Zufall.", weil Sie ja zumindest eine ungefähre Vorstellung davon haben, wie wahrscheinlich so ein Ergebnis ist. Aber das wäre dann auch schon alles, weil Sie ja aus der Statistik wissen, dass auch unwahrscheinliche Ereignisse einmal eintreten "müssen".
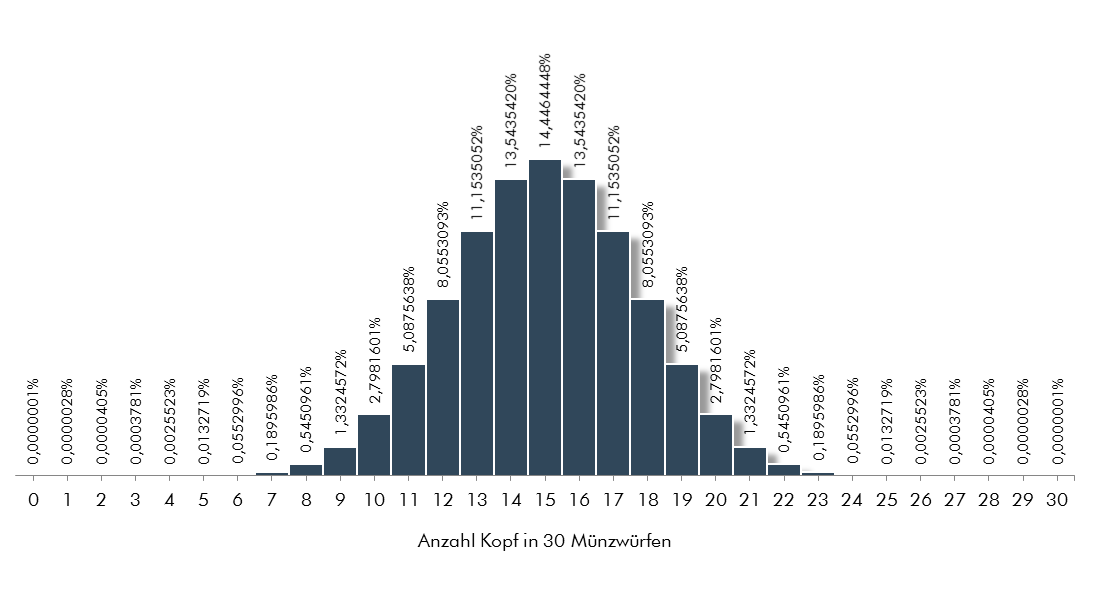
Die genaue Wahrscheinlichkeit für dieses Ergebnis kann obiger Abbildung entnommen werden. Diese beträgt für 8-mal Kopf in 30 Münzwürfen 0,545%. Werden die Wahrscheinlichkeiten von null bis acht summiert, so erhält man die Wahrscheinlichkeit für maximal 8-mal Kopf in 30 Würfen. Diese beträgt 0,806%.
Was aber würden Sie sich denken, wenn Sie die Information, dass die Münze mit einer Wahrscheinlichkeit von 50% auf Kopf bzw. Zahl fällt, vom Besitzer einer Spielhölle erhalten haben?
Wahrscheinlich würden Sie sich auch dann denken: "Was für ein Zufall." Aber jetzt würden Sie wahrscheinlich auch darüber nachdenken, ob Sie der Aussage des Besitzers basierend auf Ihrer Beobachtung weiterhin glauben (wollen). Sie werden deshalb skeptisch, weil die Münze ja angeblich mit einer Wahrscheinlichkeit von 50% auf Kopf bzw. Zahl fällt - und unter dieser Annahme dieses Ergebnis einfach sehr unwahrscheinlich ist.
Und das ist im Kern die Überlegung beim Hypothesentest, d.h.:
| 1 | Basierend auf einer Annahme machen Sie |
| 2 | eine Beobachtung und fragen sich, |
| 3 | wie wahrscheinlich es ist, unter dieser Annahme, diese konkrete Beobachtung oder eine noch unwahrscheinlichere zu machen. |
Natürlich wissen Sie, dass es sein kann, dass der Spielhöllenbesitzer die Wahrheit gesagt hat und sich seine Aussage sogar mit dem Ergebnis von 30-mal Kopf in 30 Würfen vereinbaren ließe. Aber es wird Ihnen vielleicht einfach als zu unwahrscheinlich erscheinen, weshalb Sie der Aussage keinen Glauben mehr schenken. D.h., Sie gehen nicht mehr davon aus , dass die Münze mit einer Wahrscheinlichkeit von 50% auf Kopf bzw. Zahl fällt - Sie verwerfen daher die Annahme.
Bei bzw. bis zu welchem Ergebnis Sie zwar immer noch Zweifel an der Aussage des Besitzers haben, ihm aber dann doch noch Glauben schenken wollen, ist letztlich eine Geschmacksfrage - und in der Statistik eine Frage des Signifikanzniveaus.