Die F-Verteilung
Ähnlich wie die t-Verteilung, hängt auch die Form der F-Verteilung von der Anzahl an Freiheitsgraden ab. Da jedoch die F-Verteilung das Verhältnis von zwei χ2-verteilen Variablen ist und jede χ2-verteilte Variable ihrerseits wieder durch die Anzahl an Freiheitsgraden bestimmt wird, wird die Form der F-Verteilung durch zwei "verschiedene" Freiheitsgrade bestimmt, nämlich durch die Anzahl der sog. Zähler- und Nennerfreiheitsgrade.
Nachfolgende Abbildung gibt ein Beispiel für eine F-Verteilung.
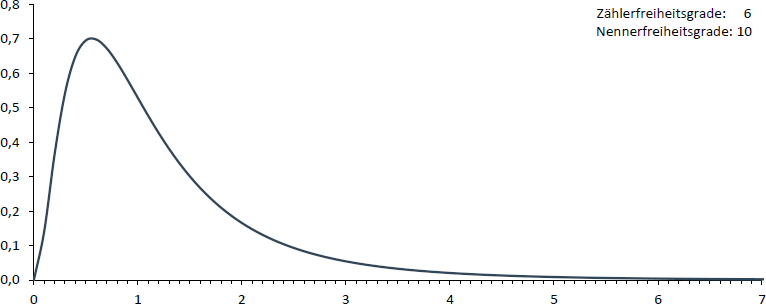
Da auf Grund dieser Tatsache die tabellarische Darstellung der F-Werte sehr umfangreich sein würde, wird an dieser Stelle gezeigt, wie in EXCEL (kritische) F-Werte bestimmt werden.
Beispiel
Stellen Sie sich vor, Sie möchten jenen F-Wert bestimmen, von dem links 95% der Fläche liegt (farbige Fläche in der folgenden Abbildung). Die Anzahl an Zählerfreiheitsgraden sei 6 und die Anzahl an Nennerfreiheitsgraden 10.
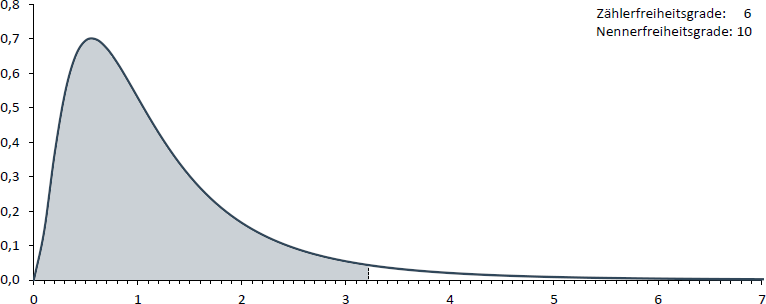
Der F-Wert kann in EXCEL mit der Funktion "=F.INV(gesuchte Fläche;Zählerfreiheitsgrade;Nennerfreiheitsgrade)" also "=F.INV(0,95;6;10)" berechnet werden und beträgt 3,22.
Wenn die Anzahl an Zählerfreiheitsgraden auf 60 und jene der Nennerfreiheitsgrade auf 100 steigt, ändert sich die Form die F-Verteilung stark, weshalb sich der F-Wert, von dem links 95% der Fläche liegt, ebenso deutlich verändert.
Nachfolgende Abbildung zeigt die entsprechende Verteilung. Der F-Wert beträgt in diesem Fall 1,45.
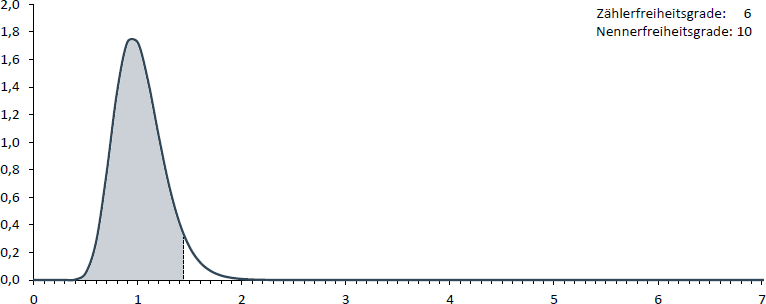
Beachten Sie, dass die untere Verteilung nicht nur deutlich schmaler ist, sondern dadurch auch deutlich höher.
Da sich die grundsätzliche Interpretation der F-Werte nicht von jener der z-Wert unterscheidet, wird für weitere Beispiele auf der Seite "Standardnormalverteilung" verwiesen.